
【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F. 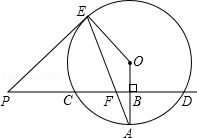
(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
(3)若PF=13,sinA= ![]() ,求EF的长.
,求EF的长.
【答案】
(1)解:连接OD,
∵直线PD垂直平分⊙O的半径OA于点B,⊙O的半径为8,
∴OB= ![]() OA=4,BC=BD=
OA=4,BC=BD= ![]() CD,
CD,
∴在Rt△OBD中,BD= ![]() =4
=4 ![]() ,
,
∴CD=2BD=8 ![]()

(2)证明:∵PE是⊙O的切线,
∴∠PEO=90°,
∴∠PEF=90°﹣∠AEO,∠PFE=∠AFB=90°﹣∠A,
∵OE=OA,
∴∠A=∠AEO,
∴∠PEF=∠PFE,
∴PE=PF
(3)解:过点P作PG⊥EF于点G,
∴∠PGF=∠ABF=90°,
∵∠PFG=∠AFB,
∴∠FPG=∠A,
∴FG=PFsinA=13× ![]() =5,
=5,
∵PE=PF,
∴EF=2FG=10.

【解析】(1)首先连接OD,由直线PD垂直平分⊙O的半径OA于点B,⊙O的半径为8,可求得OB的长,又由勾股定理,可求得BD的长,然后由垂径定理,求得CD的长;(2)由PE是⊙O的切线,易证得∠PEF=90°﹣∠AEO,∠PFE=∠AFB=90°﹣∠A,继而可证得∠PEF=∠PFE,根据等角对等边的性质,可得PE=PF;(3)首先过点P作PG⊥EF于点G,易得∠FPG=∠A,即可得FG=PFsinA=13× ![]() =5,又由等腰三角形的性质,求得答案.
=5,又由等腰三角形的性质,求得答案.


科目:初中数学 来源: 题型:
【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论: ①△AED≌△AEF;②△ABE∽△ACD;③BE+DC>DE;④BE2+DC2=DE2 , 其中正确的有( )个.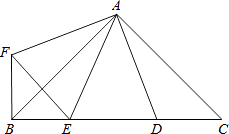
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某品牌的饮料有大瓶装与小瓶装之分.某超市花了3800元购进一批该品牌的饮料共1000瓶,其中大瓶和小瓶饮料的进价及售价如下表所示:
大瓶 | 小瓶 | |
进价(元/瓶) | 5 | 2 |
售价(元/瓶) | 7 | 3 |
(1)该超市购进大瓶和小瓶饮料各多少瓶?
(2)在大瓶饮料售出200瓶,小瓶饮料售出100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招收职员一名,从学历、经验和工作态度等三个方面对甲乙丙进行了初步测试,测试成绩如下表.
(1)如果将学历、经验和工作态度三项得分按![]() 的比例确定各人的最终得分,并以此为据确定录用者,那么谁将被录用?
的比例确定各人的最终得分,并以此为据确定录用者,那么谁将被录用?
(2)自己确定学历、经验和工作态度三项的权,并根据自己的方案确定录用者.
应聘者 | 甲 | 乙 | 丙 |
项目 | |||
学历 |
|
|
|
经验 |
|
|
|
工作态度 |
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的平面直角坐标系中有一个正六边形ABCDEF,其中C.D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A.B.C.D.E、F中,会过点(45,2)的是点 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联想与探索:
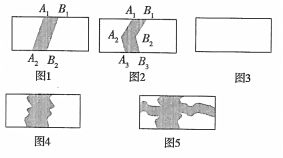
如图1,将线段A1A2本向右平移1个单位长度至B1B2,得到封闭图形A1A2B2B1(即阴影部分),在图2中,将折线A1A2A3向右平移1个单位长度至B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图3中,请你类似地画一条有两个折点的折线,同样向右平移1个单位长度,从而得到一个封闭图形,并用阴影表示;
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积(设长方形水平方向长均为a,竖直方向长均为b) :S1= ,S2= ,S3= ;
(3)如图4,在一块长方形草地上,有一条弯曲的小路(小路任何地方的水平宽度都是2个单位长度,长方形水平方向长为a,竖直方向长为b),则空白部分表示的草地面积是多少?
(4)如图5,若在(3)中的草地上又有一条横向的曲小路(小路任何地方的宽度都是1个单位长度),则空白部分表示的草地面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com