
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
【答案】(1)①安排A种产品30件,B种产品20件;②安排A种产品31件,B种产品19件;③安排A种产品32件,B种产品18件;
(2)y=﹣500x+60000, A种产品30件,B种产品20件,对应方案的利润最大,最大利润为45000元。
【解析】分析:(1)本题首先找出题中的等量关系即甲种原料不超过360千克,乙种原料不超过290千克,然后列出不等式组并求出它的解集.由此可确定出具体方案.(2)根据题意列出y与x之间的函数关系式,利用一次函数的增减性和(1)得到的取值范围即可求得最大利润.
本题解析:
(1)设生产A种产品x件,那么B种产品(50﹣x)件,则:
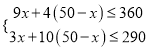 ,
,
解得:30≤x≤32,∵x为正整数,∴x=30、31、32,
依x的值分类,可设计三种方案:
①安排A种产品30件,B种产品20件;
②安排A种产品31件,B种产品19件;
③安排A种产品32件,B种产品18件.
(2)设安排生产A种产品x件,
那么利润为:y=700x+1200(50﹣x),整理得:y=﹣500x+60000,
∵k=﹣500<0,∴y随x的增大而减小,x=30、31、32,
∴当x=30时,对应方案的利润最大,y=﹣500×30+60000=45000,最大利润为45000元.
∴当安排A种产品30件,B种产品20件,对应方案的利润最大,最大利润为45000元.
点睛: 本题考查了一次函数的应用,一元一次不等式组的应用及最大利润问题,得到两种原料的关系式和总利润的等量关系是解决本题的关键.


科目:初中数学 来源: 题型:
【题目】(2016山东省聊城市第11题)如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )
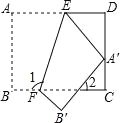
A.115° B.120° C.130° D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,![]() ≈1.732)
≈1.732)
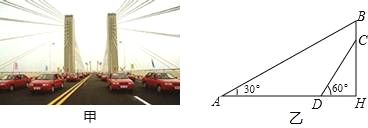
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com