
【题目】如图的平面直角坐标系中有一个正六边形ABCDEF,其中C.D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A.B.C.D.E、F中,会过点(45,2)的是点 ▲ .

科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(4,0)与y轴交于点C(0,2),抛物线的对称轴交x轴于点D.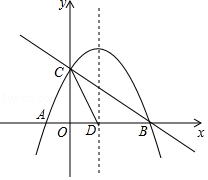
(1)求抛物线的表达式;
(2)在抛物线的对称轴是否存在点P,使△PCD是以CD为腰的等腰三角形,如果存在,求出P点的坐标,若不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?并求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F. 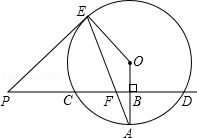
(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
(3)若PF=13,sinA= ![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是ABCD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )
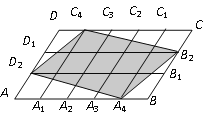
A. 4 B. ![]() C.
C. ![]() D. 30
D. 30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(a-b)2(a-b)3(b-a)5 (2)(a-b+c)3(b-a-c)5(a-b+c)6
(3)(b-a)m·(b-a)n-5·(a-b)5 (4)x·xm-1+x2·xm-2-3x3·xm-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20箱橘子,以每箱25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:

(1)20箱橘子中,最重的一箱比最轻的一箱多重多少干克?
(2)与标准重量比较,20箱橘子总计超过或不足多少千克?
(3)若橘子每千克售价2.5元,则出售这20箱橘子可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).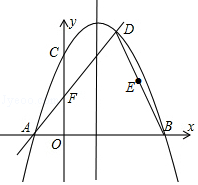
(1)求二次函数的解析式并写出D点坐标;
(2)点E是BD的中点,点Q是线段AB上一动点,当△QBE和△ABD相似时,求点Q的坐标;
(3)抛物线与y轴交于点C,直线AD与y轴交于点F,点M为抛物线对称轴上的动点,点N在x轴上,当四边形CMNF周长取最小值时,求出满足条件的点M和点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国著名数学家华罗庚曾经说过,“数形结合百般好,隔裂分家万事非。”数形结合的思想方法在数学中应用极为广泛.
观察下列按照一定规律堆砌的钢管的横截面图:
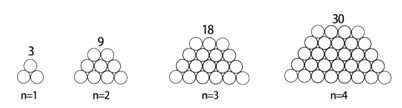
用含n的式子表示第n个图的钢管总数.
(分析思路)
图形规律中暗含数字规律,我们可以采用分步的方法,从图形排列中找规律;把图形看成几个部分的组合,并保持结构,找到每一部分对应的数字规律,进而找到整个图形对应的数字规律。
如:要解决上面问题,我们不妨先从特例入手:(统一用S表示钢管总数)
(解决问题)
(1)如图,如果把每个图形按照它的行来分割观察,你发现了这些钢管的堆砌规律了吗?像n=1、n=2的情形那样,在所给横线上,请用数学算式表达你发现的规律.

S=1+2 S=2+3+4 _____________ ______________
(2)其实,对同一个图形,我们的分析眼光可以是不同的。请你像(1)那样保持结构的、对每一个所给图形添加分割线,提供与(1)不同的分割方式;并在所给横线上,请用数学算式表达你发现的规律:

_______ ____________ _______________ _______________
(3)用含n的式子列式,并计算第n个图的钢管总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
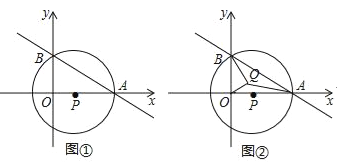
【题目】如图①,在平面直角坐标系中,直线y=kx+b与x轴正半轴交于点A,与y轴负半轴交于点B,圆心P在x轴的正半轴上,已知AB=10,AP=![]()
(1)求点P到直线AB的距离;
(2)求直线y=kx+b的解析式;
(3)在图②中存在点Q,使得∠BQO=90°,连接AQ,请求出AQ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com