练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知一组数据：1，2，6，3，3，下列说法错误的是（ ）
    A.众数是3
    B.中位数是6
    C.平均数是3
    D.方差是2.8

    【答案】B
    【解析】解：A、3出现了2次，出现的次数最多，则众数是3，故本选项正确；
    B、把这组数据从小到大排列为：1，2，3，3，6，最中间的数是3，则中位数是3，故本选项错误；
    C、这组数据的平均数是（1+2+6+3+3）÷5=3，故本选项正确；
    D、这组数据的方差是： [（1﹣3）2+（2﹣3）2+（6﹣3）2+（3﹣3）2+（3﹣3）2]= ，故本选项正确；
    故选B．
    【考点精析】认真审题，首先需要了解中位数、众数(中位数是唯一的，仅与数据的排列位置有关，它不能充分利用所有数据；众数可能一个，也可能多个，它一定是这组数据中的数)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

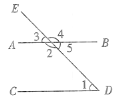
    【题目】如图,直线AB，CD被DE所截，则∠1和 是同位角，∠1和 是内错角，∠1和 是同旁内角；

    (2)在(1)中，如果∠5=∠1,那么∠1=∠3的推理过程如下,请在括号内注明理由：

    因为∠5=∠1( )，

    ∠5=∠3( )，

    所以∠1=∠3( ).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一条南北方向的公路上，有一辆出租车停在A地，乘车的第一位客人向南走3千米下车；该车继续向南开，又走了2千米后，上来第二位客人，第二位客人乘车向北走7千米下车，此时恰好有第三位客人上车，先向北走3千米，又调头向南走，结果下车时出租车恰好到了A地．

    （1）如果以A地为原点，向北方向为正方向，用1个单位表示1千米，在数轴上表示出第一位客人和第二位客人下车的位置；

    （2）第三位客人乘车走了多少千米？

    （3）规定出租车的收费标准是4千米内付7元，超过4千米的部分每千米加付1元（不足1千米按1千米算），那么该出租车司机在这三位客人中共收了多少钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面材料：已知点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为|AB|．

    当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|＝|OB|＝|b|＝|a﹣b|

    当A、B两点都不在原点时，

    （1）如图2，点A、B都在原点的右边，|AB|＝|OB|﹣|OA|＝|b|﹣|a|＝b﹣a＝|a﹣b|

    （2）如图3，点A、B都在原点的左边，|AB|＝|OB|﹣|OA|＝|b|﹣|a|＝﹣b﹣（﹣a）＝a﹣b＝|a﹣b|

    （3）如图4，点A、B在原点的两边，|AB|＝|OA|+|OB|＝|a|+|b|＝a+（﹣b）＝a﹣b＝|a﹣b|

    综上，数轴上A、B两点的距离|AB|＝|a﹣b|

    回答下列问题：

    （1）数轴上表示﹣2和﹣5两点之间的距离是多少；

    （2）数轴上表示x和﹣1的两点A、B之间的距离是|x+1|，如果|AB|＝2，那么x为多少；

    （3）当代数式|x+1|+|x﹣2|取最小值时，写出相应的x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知直线PD垂直平分⊙O的半径OA于点B，PD交⊙O于点C、D，PE是⊙O的切线，E为切点，连结AE，交CD于点F．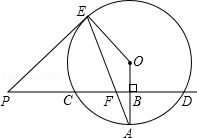
    （1）若⊙O的半径为8，求CD的长；
    （2）证明：PE=PF；
    （3）若PF=13，sinA= ，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，从①∠1＝∠2；②∠C＝∠D；③∠A＝∠F三个条件中选出两个作为已知条件，另一个作为结论所组成的命题中，正确命题的个数为( )

    A. 0 B. 1 C. 2 D. 3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

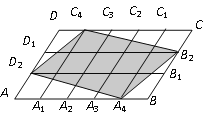
    【题目】如图，在平行四边形ABCD中，点A1，A2，A3，A4和C1，C2，C3，C4分别是ABCD的五等分点，点B1，B2和D1，D2分别是BC和DA的三等分点，已知四边形A4B2C4D2的面积为2，则平行四边形ABCD的面积为（ ）

    A. 4 B. C. D. 30

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有20箱橘子,以每箱25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:

    (1)20箱橘子中,最重的一箱比最轻的一箱多重多少干克?

    (2)与标准重量比较,20箱橘子总计超过或不足多少千克?

    (3)若橘子每千克售价2.5元,则出售这20箱橘子可卖多少元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△AOB和Rt△COD中，∠AOB=∠COD=90°，∠B=40°，∠C=60°，点D在边OA上，将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，在第 秒时，边CD恰好与边AB平行．

    查看答案和解析>>

    同步练习册答案