
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4),以A为顶点的抛物线y=ax2+bx+c过点C,动点P从点A出发,以每秒 ![]() 个单位的速度沿线段AD向点D运动,运动时间为t秒,过点P作PE⊥x轴交抛物线于点M,交AC于点N.
个单位的速度沿线段AD向点D运动,运动时间为t秒,过点P作PE⊥x轴交抛物线于点M,交AC于点N.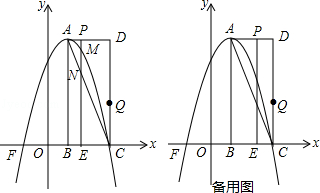
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)当t为何值时,△ACM的面积最大?最大值为多少?
(3)点Q从点C出发,以每秒1个单位的速度沿线段CD向点D运动,当t为何值时,在线段PE上存在点H,使以C,Q,N,H为顶点的四边形为菱形?
【答案】
(1)
解:(1)A(1,4),
由题意知,可设抛物线解析式为y=a(x﹣1)2+4
∵抛物线过点C(3,0),
∴0=a(3﹣1)2+4,
解得a=﹣1.
∴抛物线的解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3;
(2)
解:如图1,
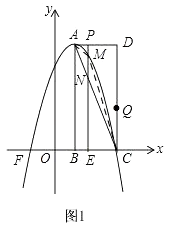
∵A(1,4),C(3,0),
∴可求直线AC的解析式为y=﹣2x+6.
∵点P(1+ ![]() ,4).
,4).
∴将x=1+ ![]() 代入y=﹣2x+6中,解得点N的纵坐标为y=4﹣t,
代入y=﹣2x+6中,解得点N的纵坐标为y=4﹣t,
∴把x=1+ ![]() ,代入抛物线的解析式中,可求点M的纵坐标为4﹣
,代入抛物线的解析式中,可求点M的纵坐标为4﹣ ![]() ,
,
∴MN=(4﹣ ![]() )﹣(4﹣t)=t﹣
)﹣(4﹣t)=t﹣ ![]() ,
,
又点A到MN的距离为 ![]() ,C到MN的距离为2﹣
,C到MN的距离为2﹣ ![]() ,
,
即S△ACM=S△AMN+S△CMN= ![]() ×MN×
×MN× ![]() +
+ ![]() ×MN×(2﹣
×MN×(2﹣ ![]() )
)
= ![]() ×2(t﹣
×2(t﹣ ![]() )=﹣
)=﹣ ![]() (t﹣2)2+1.
(t﹣2)2+1.
当t=2时,S△ACM的最大值为1.
(3)
解:由题意和(2)知,(3,0),Q(3,t),N( ![]() ,4﹣t),AB=4,
,4﹣t),AB=4,
AG=4﹣(4﹣t)=t,BG=4﹣t,可求AC= ![]() ,
,
当H在AC上方时,如图2,过点N作NG⊥AB,
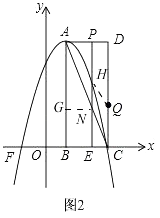
由四边形CQNH是菱形,可知:CQ=CN=t,
此时,AN= ![]() ﹣t,NG∥BC,
﹣t,NG∥BC,
∴ ![]() ,
,
![]() ,
,
解得:t=20﹣ ![]() ,
,
当点H在AC下方时,如图3,
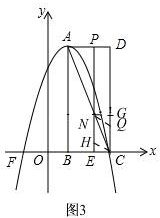
由四边形CQNH是菱形,可知:CH=HN=CQ=t,
∴HE=4﹣t﹣t=4﹣2t,EC=2﹣ ![]() ,
,
在直角三角形CHE中,CE2+HE2=CH2,
∴ ![]() ,
,
解得t= ![]() 或t=4(舍去),
或t=4(舍去),
所以,以C,Q,N,H为顶点的四边形为菱形时,t= ![]() 或t=20﹣8
或t=20﹣8 ![]() .
.
【解析】(1)根据矩形的性质可以写出点A的坐标;由顶点A的坐标可设该抛物线的顶点式方程为y=a(x﹣1)2+4,然后将点C的坐标代入,即可求得系数a的值;(2)利用待定系数法求得直线AC;由图形与坐标变换可以求得点P的坐标,进一步表示点M,N的坐标,得出面积关于t的二次函数,由二次函数的最值可以求解;(3)因为菱形是邻边相等的平行四边形,所以点H在直线EF上,分CH是边和对角线两种情况讨论即可.
【考点精析】掌握平行四边形的性质和矩形的性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;矩形的四个角都是直角,矩形的对角线相等.


科目:初中数学 来源: 题型:
【题目】某公司欲招收职员一名,从学历、经验和工作态度等三个方面对甲乙丙进行了初步测试,测试成绩如下表.
(1)如果将学历、经验和工作态度三项得分按![]() 的比例确定各人的最终得分,并以此为据确定录用者,那么谁将被录用?
的比例确定各人的最终得分,并以此为据确定录用者,那么谁将被录用?
(2)自己确定学历、经验和工作态度三项的权,并根据自己的方案确定录用者.
应聘者 | 甲 | 乙 | 丙 |
项目 | |||
学历 |
|
|
|
经验 |
|
|
|
工作态度 |
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ![]() ,反比例函数y=
,反比例函数y= ![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( ) 
A.60
B.80
C.30
D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联想与探索:
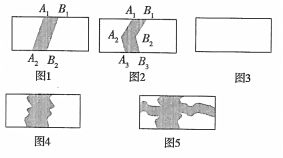
如图1,将线段A1A2本向右平移1个单位长度至B1B2,得到封闭图形A1A2B2B1(即阴影部分),在图2中,将折线A1A2A3向右平移1个单位长度至B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图3中,请你类似地画一条有两个折点的折线,同样向右平移1个单位长度,从而得到一个封闭图形,并用阴影表示;
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积(设长方形水平方向长均为a,竖直方向长均为b) :S1= ,S2= ,S3= ;
(3)如图4,在一块长方形草地上,有一条弯曲的小路(小路任何地方的水平宽度都是2个单位长度,长方形水平方向长为a,竖直方向长为b),则空白部分表示的草地面积是多少?
(4)如图5,若在(3)中的草地上又有一条横向的曲小路(小路任何地方的宽度都是1个单位长度),则空白部分表示的草地面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在大楼45米高(即PH=45米,且PH⊥HC)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处得俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: ![]() .(点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上)
.(点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上)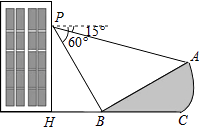
(1)∠PBA的度数等于度;(直接填空)
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
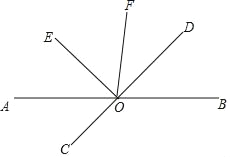
【题目】如图,直线AB、CD相交于点O,OE⊥OD,OE平分∠AOF.
(1)∠BOD与∠DOF相等吗?请说明理由.
(2)若∠DOF=![]() ∠BOE,求∠AOD的度数.
∠BOE,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⑴ 一个数的平方等于它的本身的数是____________
⑵ 平方根等于它的本身的数是______________
⑶ 算术平方根等于它的本身的数是__________
⑷ 立方根等于它的本身的数是______________
⑸ 大于0且小于π的整数是________________
⑹ 满足![]() <x <
<x <![]() 的整数x是_______
的整数x是_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁): 39 35 33 39 27 33 35 31 31 37 32 38 36 31 39 32 38 37
34 34 38 32 35 36 33 32 35 36 37 39 38 40 38 37 39 38
34 33 40 36 36 37 31 38 38 37 35 40 39 37
请根据以上数据,解答以下问题:
(1)小彬按“组距为5”列出了如下的频数分布表,每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图:
分组 | 频数 |
A:25~30 | |
B:30~35 | 15 |
C:35~40 | 31 |
D:40~45 | |
总 计 | 50 |
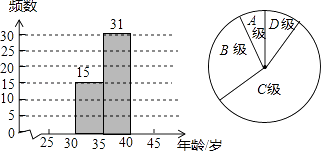
(2)在(1)的基础上,小彬又画出了如图所示的扇形统计图,图中B组所对的圆心角的度数为;
(3)根据(1)中的频数分布直方图试描述这50位菲尔兹奖得主获奖时的年龄的分布特征.
查看答案和解析>>
科目:初中数学 来源: 题型:
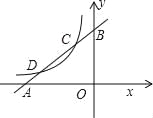
【题目】如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线![]() (x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(1)分别求出直线AB及双曲线的解析式;
(2)求出点D的坐标;
(3)利用图象直接写出:当x在什么范围内取值时,y1>y2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com