
【题目】菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁): 39 35 33 39 27 33 35 31 31 37 32 38 36 31 39 32 38 37
34 34 38 32 35 36 33 32 35 36 37 39 38 40 38 37 39 38
34 33 40 36 36 37 31 38 38 37 35 40 39 37
请根据以上数据,解答以下问题:
(1)小彬按“组距为5”列出了如下的频数分布表,每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图:
分组 | 频数 |
A:25~30 | |
B:30~35 | 15 |
C:35~40 | 31 |
D:40~45 | |
总 计 | 50 |
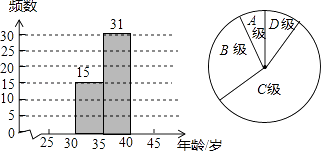
(2)在(1)的基础上,小彬又画出了如图所示的扇形统计图,图中B组所对的圆心角的度数为;
(3)根据(1)中的频数分布直方图试描述这50位菲尔兹奖得主获奖时的年龄的分布特征.
【答案】
(1)解:如图所示:
分组 | 频数 |
A:25~30 | 1 |
B:30~35 | 15 |
C:35~40 | 31 |
D:40~45 | 3 |
总 计 | 50 |
频数分布直方图如下:
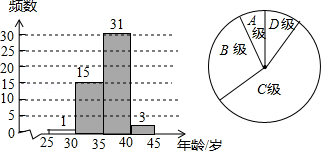
(2)108°
(3)解:由频数分布直方图知,这56位菲尔兹奖得主获奖时的年龄主要分布在35~40岁
【解析】解:(1)补全频数分布直方图如下:
分组 | 频数 |
A:25~30 | 1 |
B:30~35 | 15 |
C:35~40 | 31 |
D:40~45 | 3 |
总 计 | 50 |
补全频数分布直方图如下:
所以答案是:1、3.
⑵图中B组所对的圆心角的度数为360° ![]() =108°,
=108°,
所以答案是:108°;
【考点精析】解答此题的关键在于理解频数分布直方图的相关知识,掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图),以及对扇形统计图的理解,了解能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).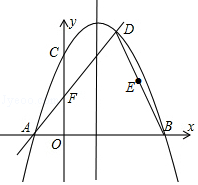
(1)求二次函数的解析式并写出D点坐标;
(2)点E是BD的中点,点Q是线段AB上一动点,当△QBE和△ABD相似时,求点Q的坐标;
(3)抛物线与y轴交于点C,直线AD与y轴交于点F,点M为抛物线对称轴上的动点,点N在x轴上,当四边形CMNF周长取最小值时,求出满足条件的点M和点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4),以A为顶点的抛物线y=ax2+bx+c过点C,动点P从点A出发,以每秒 ![]() 个单位的速度沿线段AD向点D运动,运动时间为t秒,过点P作PE⊥x轴交抛物线于点M,交AC于点N.
个单位的速度沿线段AD向点D运动,运动时间为t秒,过点P作PE⊥x轴交抛物线于点M,交AC于点N.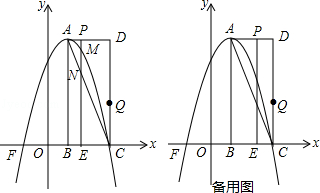
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)当t为何值时,△ACM的面积最大?最大值为多少?
(3)点Q从点C出发,以每秒1个单位的速度沿线段CD向点D运动,当t为何值时,在线段PE上存在点H,使以C,Q,N,H为顶点的四边形为菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
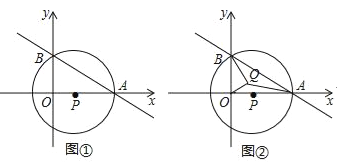
【题目】如图①,在平面直角坐标系中,直线y=kx+b与x轴正半轴交于点A,与y轴负半轴交于点B,圆心P在x轴的正半轴上,已知AB=10,AP=![]()
(1)求点P到直线AB的距离;
(2)求直线y=kx+b的解析式;
(3)在图②中存在点Q,使得∠BQO=90°,连接AQ,请求出AQ的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
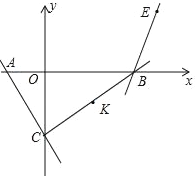
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x﹣
x﹣![]() 交x轴于点A,交y轴于点C,直线y=
交x轴于点A,交y轴于点C,直线y=![]() x﹣5
x﹣5![]() 交x轴于点B,在平面内有一点E,其坐标为(4,
交x轴于点B,在平面内有一点E,其坐标为(4,![]() ),连接CB,点K是线段CB的中点,另有两点M,N,其坐标分别为(a,0),(a+1,0).将K点先向左平移
),连接CB,点K是线段CB的中点,另有两点M,N,其坐标分别为(a,0),(a+1,0).将K点先向左平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位得K′,当以K′,E,M,N四点为顶点的四边形周长最短时,a的值为_____.
个单位得K′,当以K′,E,M,N四点为顶点的四边形周长最短时,a的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知数轴上有三点A、B、C,它们对应的数分别为a、b、c,且c-b=b-a;点C对应的数是10.
(1)若BC=15,求a、b的值;
(2)如图2,在(1)的条件下,O为原点,动点P、Q分别从A、C同时出发,点P向左运动,运动速度为2个单位长度/秒,点Q向右运动,运动速度为1个单位长度/秒,N为OP的中点,M为BQ的中点.
①用含t代数式表示PQ、 MN;
②在P、Q的运动过程中,PQ与MN存在一个确定的等量关系,请指出他们之间的关系,并说明理由.
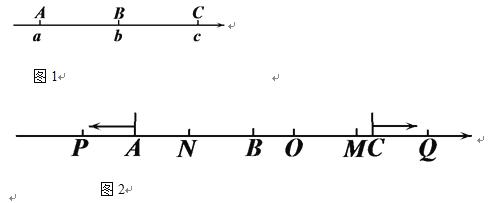
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连结AE,当△ABE时等腰三角形时,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数![]() (x>0)的图像与△ABC有公共点,则k的取值范围是( )
(x>0)的图像与△ABC有公共点,则k的取值范围是( )

A. 2≤k≤9 B. 2≤k≤8 C. 2≤k≤5 D. 5≤k≤8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F在AC上,AD=BC,AD//BC,则添加下列哪个条件后,仍无法判定△ADF≌△CBE的是
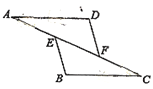
A. DF=BE B. ∠D=∠B C. AE=CF D. DF//BE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com