
【题目】如图,点E、F在AC上,AD=BC,AD//BC,则添加下列哪个条件后,仍无法判定△ADF≌△CBE的是
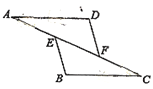
A. DF=BE B. ∠D=∠B C. AE=CF D. DF//BE
【答案】A
【解析】
根据全等三角形的判定方法逐项分析即可.
∵AD//BC,
∴∠A=∠C.
A. 若添加DF=BE,不符合全等三角形的判定方法,故符合题意;
B. 若添加∠D=∠B,
在△ADF和△CBE中,
∵∠A=∠C,
AD=BC,
D=∠B,
∴△ADF≌△CBE(ASA),故不符合题意;
C. 若添加AE=CF ,则AF=CE,
在△ADF和△CBE中,
∵AF=CE,
∠A=∠C,
AD=BC,
∴△ADF≌△CBE(SAS),故不符合题意;
D. 若添加 DF//BE,则∠AFD=∠CEB,
在△ADF和△CBE中,
∵∠A=∠C,
∠AFD=∠CEB,
AD=BC,
∴△ADF≌△CBE(AAS),故不符合题意;
故选A.


科目:初中数学 来源: 题型:
【题目】菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁): 39 35 33 39 27 33 35 31 31 37 32 38 36 31 39 32 38 37
34 34 38 32 35 36 33 32 35 36 37 39 38 40 38 37 39 38
34 33 40 36 36 37 31 38 38 37 35 40 39 37
请根据以上数据,解答以下问题:
(1)小彬按“组距为5”列出了如下的频数分布表,每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图:
分组 | 频数 |
A:25~30 | |
B:30~35 | 15 |
C:35~40 | 31 |
D:40~45 | |
总 计 | 50 |
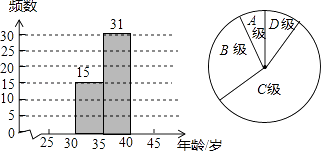
(2)在(1)的基础上,小彬又画出了如图所示的扇形统计图,图中B组所对的圆心角的度数为;
(3)根据(1)中的频数分布直方图试描述这50位菲尔兹奖得主获奖时的年龄的分布特征.
查看答案和解析>>
科目:初中数学 来源: 题型:
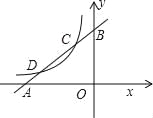
【题目】如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线![]() (x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(1)分别求出直线AB及双曲线的解析式;
(2)求出点D的坐标;
(3)利用图象直接写出:当x在什么范围内取值时,y1>y2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一根绳子对折成一条线段AB,在线段AB取一点P,使AP=![]() ,从P处把绳子剪断,若剪断后的三段绳子中最长的一段为30cm,则绳子的原长为______cm.
,从P处把绳子剪断,若剪断后的三段绳子中最长的一段为30cm,则绳子的原长为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请仅用无刻度的直尺在下列图1和图2中按要求画菱形. 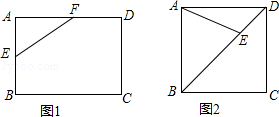
(1)图1是矩形ABCD,E,F分别是AB和AD的中点,以EF为边画一个菱形;
(2)图2是正方形ABCD,E是对角线BD上任意一点(BE>DE),以AE为边画一个菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
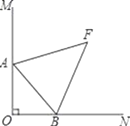
【题目】如图,∠MON=90°,OB=2,点A是直线OM上的一个动点,连结AB,作∠MAB与∠ABN的角平分线AF与BF,两角平分线所在的直线交于点F,求点A在运动过程中线段BF的最小值为 ______
查看答案和解析>>
科目:初中数学 来源: 题型:
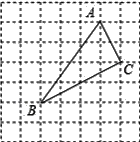
【题目】如图,在7×7网格中,每个小正方形的边长都为1.
(1)建立适当的平面直角坐标系后,若点A(3,4)、C(4,2),则点B的坐标为 ;
(2)图中格点△ABC的面积为 ;
(3)判断格点△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
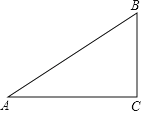
【题目】如图,Rt△ABC中,∠C=90°,AC=8,BC=6.
(1)尺规作图:作△BAC的角平分线AD(保留作图痕迹,不写作法);
(2)求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
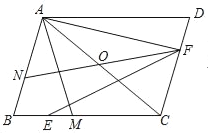
【题目】如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N.
(1)若BM=4,MC=3,AC=![]() ,求AM的长度;
,求AM的长度;
(2)若∠ACB=45°,求证:AN+AF=![]() EF.
EF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com