
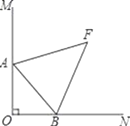
【题目】如图,∠MON=90°,OB=2,点A是直线OM上的一个动点,连结AB,作∠MAB与∠ABN的角平分线AF与BF,两角平分线所在的直线交于点F,求点A在运动过程中线段BF的最小值为 ______
科目:初中数学 来源: 题型:
【题目】如图1,已知数轴上有三点A、B、C,它们对应的数分别为a、b、c,且c-b=b-a;点C对应的数是10.
(1)若BC=15,求a、b的值;
(2)如图2,在(1)的条件下,O为原点,动点P、Q分别从A、C同时出发,点P向左运动,运动速度为2个单位长度/秒,点Q向右运动,运动速度为1个单位长度/秒,N为OP的中点,M为BQ的中点.
①用含t代数式表示PQ、 MN;
②在P、Q的运动过程中,PQ与MN存在一个确定的等量关系,请指出他们之间的关系,并说明理由.
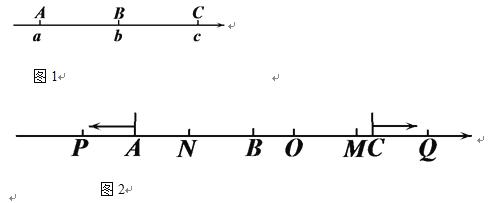
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市为加快美丽乡村建设,建设秀美幸福宿州,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元;甲镇建设了2个A类村庄和5个B类村庄共投入资金1140万元.
(1)建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?
(2)乙镇3个A类美丽村庄和6个B类村庄改建共需资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育中考前,抽样调查了九年级学生的“1分钟跳绳”成绩,并绘制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图. 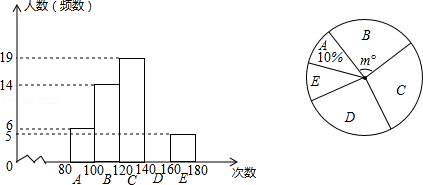
(1)补全频数分布直方图;
(2)扇形图中m=;
(3)若“1分钟跳绳”成绩大于或等于140次为优秀,则估计全市九年级5900名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F在AC上,AD=BC,AD//BC,则添加下列哪个条件后,仍无法判定△ADF≌△CBE的是
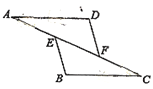
A. DF=BE B. ∠D=∠B C. AE=CF D. DF//BE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
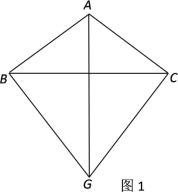
【题目】如图1,在△ABC中,AB=AC,G为三角形外一点,且△GBC为等边三角形.
(1)求证:直线AG垂直平分BC;
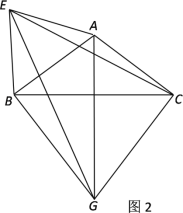
(2)以AB为一边作等边△ABE(如图2),连接EG、EC,试判断△EGC是否构成直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得![]() ,(x、y为正整数)∴
,(x、y为正整数)∴![]() 则有0<x<6.又
则有0<x<6.又![]() 为正整数,则
为正整数,则![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入![]() =2.
=2.
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解:_____;
(2)若![]() 为自然数,则满足条件的整数x值有_____个;
为自然数,则满足条件的整数x值有_____个;
A、2 B、3 C、4 D、5
查看答案和解析>>
科目:初中数学 来源: 题型:
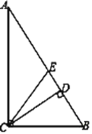
【题目】如图,在Rt△ABC中,∠ACB=90°,CD与CE分别是斜边AB上的高与中线,则下列结论:①BE=BC;②∠DCB=∠A;③∠DCB=∠ACE;④![]() ,其中正确的结论是_____.
,其中正确的结论是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com