
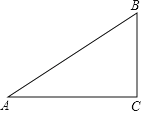
【题目】如图,Rt△ABC中,∠C=90°,AC=8,BC=6.
(1)尺规作图:作△BAC的角平分线AD(保留作图痕迹,不写作法);
(2)求AD的长.
科目:初中数学 来源: 题型:
【题目】如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数![]() (x>0)的图像与△ABC有公共点,则k的取值范围是( )
(x>0)的图像与△ABC有公共点,则k的取值范围是( )

A. 2≤k≤9 B. 2≤k≤8 C. 2≤k≤5 D. 5≤k≤8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F在AC上,AD=BC,AD//BC,则添加下列哪个条件后,仍无法判定△ADF≌△CBE的是
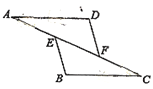
A. DF=BE B. ∠D=∠B C. AE=CF D. DF//BE
查看答案和解析>>
科目:初中数学 来源: 题型:
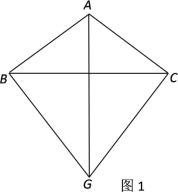
【题目】如图1,在△ABC中,AB=AC,G为三角形外一点,且△GBC为等边三角形.
(1)求证:直线AG垂直平分BC;
(2)以AB为一边作等边△ABE(如图2),连接EG、EC,试判断△EGC是否构成直角三角形?请说明理由.
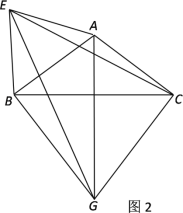
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得![]() ,(x、y为正整数)∴
,(x、y为正整数)∴![]() 则有0<x<6.又
则有0<x<6.又![]() 为正整数,则
为正整数,则![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入![]() =2.
=2.
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解:_____;
(2)若![]() 为自然数,则满足条件的整数x值有_____个;
为自然数,则满足条件的整数x值有_____个;
A、2 B、3 C、4 D、5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校“百变魔方”社团准备购买![]() ,
,![]() 两种魔方.已知购买2个
两种魔方.已知购买2个![]() 种魔方和6个
种魔方和6个![]() 种魔方共需130元,购买3个
种魔方共需130元,购买3个![]() 种魔方和4个
种魔方和4个![]() 种魔方所需款数相同.
种魔方所需款数相同.
(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买![]() ,
,![]() 两种魔方共100个(其中
两种魔方共100个(其中![]() 种魔方不超过50个).某商店有两种优惠活动,如图所示.
种魔方不超过50个).某商店有两种优惠活动,如图所示.
请根据以上信息,说明选择哪种优惠活动购买魔方更实惠.

查看答案和解析>>
科目:初中数学 来源: 题型:
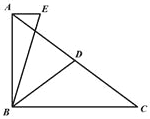
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,D为AC中点,过点A作AE∥BC,连结BE,∠EBD=∠CBD,BD=5,则BE的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
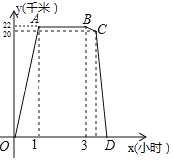
【题目】某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.
(1)活动中心与小宇家相距 千米,小宇在活动中心活动时间为 小时,他从活动中心返家时,步行用了 小时;
(2)求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);
(3)根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com