
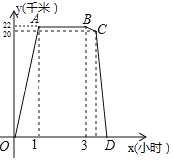
����Ŀ��ij��������8��00С��Ӽҳ������˳�1Сʱ����ij����IJμ�ʵ�����11��00ʱ���ڻ���Ľӵ��ְֵĵ绰������Ҫ������12��00ǰ�ص��ң������̰����������ʱ��·�ߣ���5ǧ��/Сʱ��ƽ���ٶȿ첽���أ�ͬʱ���ְִӼ���ͬһ·�߿����������ھ��20ǧ�״�������С���������ԭ���ij���ԭ·���أ���С�����x��Сʱ���������y��ǧ�ף��ĵط���ͼ������OABCD��ʾy��x֮��ĺ�����ϵ��
��1���������С������ ǧ�ף�С���ڻ���Ļʱ��Ϊ Сʱ�����ӻ���ķ���ʱ���������� Сʱ��
��2�����߶�BC����ʾ��y��ǧ�ף���x��Сʱ��֮��ĺ�����ϵʽ������д��x����ʾ�ķ�Χ����
��3����������������������������أ������ж�С���Ƿ�����12��00ǰ�ص��ң���˵�����ɣ�
���𰸡���1��22��2��0.4����2��y=��5x+37����3����.
��������
�����������1�����ݵ�A��B������ʱ��=·�����ٶȣ����ɵó����ۣ�
��2��������Ҿ���=22���ٶ���ʱ�䣬���ɵó�y��x֮��ĺ�����ϵʽ��
��3����С��е�ʱ����ڰְֿ����ӵ�С���ʱ��������ʱ����ͬ���������С��ӻ���ķ�������ʱ�䣬������1�ȽϺɵó����ۣ�
�����������1������A��������1��22������B��������3��22����
���������С������22ǧ�ף�С���ڻ���Ļʱ��Ϊ3��1=2Сʱ��
��22��20����5=0.4��Сʱ����
��2����������ã�y=22��5��x��3��=��5x+37��
��3��С��ӻ���ķ�������ʱ��Ϊ��0.4+0.4=0.8��Сʱ����
��0.8��1��
������С��12��00ǰ�ܵ��ң�


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
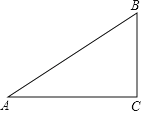
����Ŀ����ͼ��Rt��ABC�У���C=90�㣬AC=8��BC=6��
��1���߹���ͼ������BAC�Ľ�ƽ����AD��������ͼ�ۼ�����д��������
��2����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
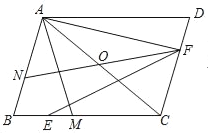
����Ŀ����ͼ��ƽ���ı���ABCD�У���O�ǶԽ���AC���е㣬��MΪBC��һ�㣬����AM����AB=AM����EΪBM�е㣬AF��AB������EF���ӳ�FO��AB�ڵ�N��
��1����BM=4��MC=3��AC=![]() ����AM�ij��ȣ�
����AM�ij��ȣ�
��2������ACB=45������֤��AN+AF=![]() EF��
EF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=kx+b��![]() ����y=-4x��
����y=-4x��![]() ����ͼ���ཻ�ڵ�P��1,n��,��C(3,2)��һ�κ���ͼ����
����ͼ���ཻ�ڵ�P��1,n��,��C(3,2)��һ�κ���ͼ����
����k��b��ֵ��
��ֱ��д��kx+b>-4x�Ľ⼯
������OC����������OPC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
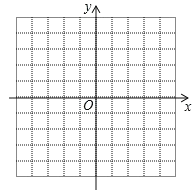
����Ŀ����ƽ��ֱ������ϵ������� A����2��0����B��3��1����C��2��3�������������߶����� ����������������������⣺
��1����ƽ��ֱ������ϵ�л����� A��B��C����ʹ������ ABC ���� x ��Գƣ���ֱ��д���� A��B��C�����������������
��2������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ��̽����
��1����ͼ1�����۾���ֽƬABCD��ʹAD��BC�غϣ��õ��ۺ�EF����ֽƬչ������һ���۵�ֽƬ��ʹ��A����EF�ϣ���ʹ�ۺ۾�����B���õ��ۺ�BM��ͬʱ�õ��߶�BN��MN.����۲�ͼ1�������MBN�Ķ����Ƕ��٣���֤����Ľ���. 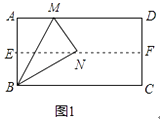
��2����ͼ1�е�������ֽƬBMN���£���ͼ2���۵���ֽƬ��̽��MN��BM��������ϵ��д���۵�����������Ϸ���֤����Ľ���. 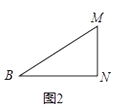
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������֤�����̣�
��ͼ����1����2��ACƽ�֡�DAB.
![]()
��֤��DC��AB.
֤������ΪACƽ�֡�DAB(��֪)��
���ԡ�1����3(_____________ )��
������1����2(____________)��
���ԡ�2����3(______________)��
����DC��AB(________________)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC����C=90�㣬DΪBC���е㣬��ACΪֱ���ġ�O��AB�ڵ�E�� 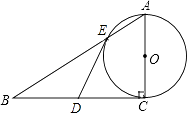
��1����֤��DE�ǡ�O�����ߣ�
��2����AE��EB=1��2��BC=6����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ��ʦ������һ��˼���⡰���㣺��-![]() ����(
����(![]()
![]() )����С����ϸ˼����һ��������һ�ֲ�ͬ�ķ��������������⣮
)����С����ϸ˼����һ��������һ�ֲ�ͬ�ķ��������������⣮
С���Ľⷨ��ԭʽ�ĵ���Ϊ(![]()
![]() )��(
)��(![]() )=(
)=(![]()
![]() )����-12��=-4+10=6�����ԣ�-
)����-12��=-4+10=6�����ԣ�-![]() ����(
����(![]()
![]() )=
)=![]() ��
��
(1)�����ж�С���Ľ���Ƿ���ȷ����˵�����ɣ�
(2)��������С���Ľⷨ�����������⣮
���㣺��-![]() ����(
����(![]()
![]() +
+![]() )��
)��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com