
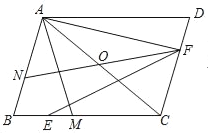
【题目】如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N.
(1)若BM=4,MC=3,AC=![]() ,求AM的长度;
,求AM的长度;
(2)若∠ACB=45°,求证:AN+AF=![]() EF.
EF.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)连接AE.根据等腰三角形的性质得到,AE⊥BM,根据勾股定理求出
![]()
![]() 即可得解.
即可得解.
(2)连接AE,作EH⊥AF于F,EG⊥DC交DC的延长线于E.根据∠AEC=∠AFC=90°,∠AEC+∠AFC=90°,得到A,E,C,F四点共圆,根据圆周角定理得到∠AFE=∠ACE=45°,继而得到∠EFA=∠EFG=45°,根据等腰直角三角形的性质得到EH=EG,AE=EC,证明Rt△EHA≌Rt△EGC,Rt△EHF≌Rt△EGF,△AON≌△COF根据全等三角形的性质得到,AN=CF,AN+AF=FC+AF=FG﹣CG+FH+AH=2FH,根据![]() 即可证明.
即可证明.
(1)解:如图1中,连接AE.
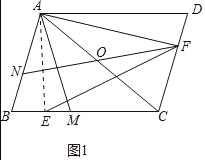
∵AB=AM,BE=EM,
∴AE⊥BM,
在Rt△ACE中,∵AC=![]() ,EC=EM+CM=5,
,EC=EM+CM=5,
∴![]()
在Rt△AEM中,![]()
(2)如图,连接AE,作EH⊥AF于F,EG⊥DC交DC的延长线于E.
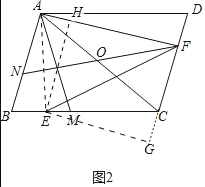
∵∠AEC=∠AFC=90°,
∴∠AEC+∠AFC=90°,
∴A,E,C,F四点共圆,
∴∠AFE=∠ACE=45°,
∴∠EFA=∠EFG=45°,
∵EH⊥FA,EG⊥FG,
∴EH=EG,
∵∠ACE=∠EAC=45°,
∴AE=EC,
∴Rt△EHA≌Rt△EGC(HL),
∴AH=CG,
∵EF=EF,EH=EG,
∴Rt△EHF≌Rt△EGF(HL),
∴FH=FG,
∵AB∥CD,
∴∠OAN=∠OCF,
∵∠AON=∠COF,OA=OC,
∴△AON≌△COF(ASA),
∴AN=CF,
∴AN+AF=FC+AF=FG﹣CG+FH+AH=2FH,
∵![]()
∴![]()


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点E、F在AC上,AD=BC,AD//BC,则添加下列哪个条件后,仍无法判定△ADF≌△CBE的是
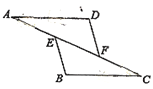
A. DF=BE B. ∠D=∠B C. AE=CF D. DF//BE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校“百变魔方”社团准备购买![]() ,
,![]() 两种魔方.已知购买2个
两种魔方.已知购买2个![]() 种魔方和6个
种魔方和6个![]() 种魔方共需130元,购买3个
种魔方共需130元,购买3个![]() 种魔方和4个
种魔方和4个![]() 种魔方所需款数相同.
种魔方所需款数相同.
(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买![]() ,
,![]() 两种魔方共100个(其中
两种魔方共100个(其中![]() 种魔方不超过50个).某商店有两种优惠活动,如图所示.
种魔方不超过50个).某商店有两种优惠活动,如图所示.
请根据以上信息,说明选择哪种优惠活动购买魔方更实惠.

查看答案和解析>>
科目:初中数学 来源: 题型:
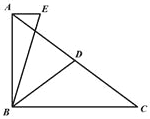
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,D为AC中点,过点A作AE∥BC,连结BE,∠EBD=∠CBD,BD=5,则BE的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
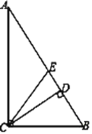
【题目】如图,在Rt△ABC中,∠ACB=90°,CD与CE分别是斜边AB上的高与中线,则下列结论:①BE=BC;②∠DCB=∠A;③∠DCB=∠ACE;④![]() ,其中正确的结论是_____.
,其中正确的结论是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
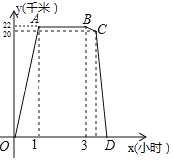
【题目】某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.
(1)活动中心与小宇家相距 千米,小宇在活动中心活动时间为 小时,他从活动中心返家时,步行用了 小时;
(2)求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);
(3)根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( ) 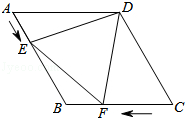
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com