
【题目】如图,直线AB、CD相交于点O,OE⊥OD,OE平分∠AOF.
(1)∠BOD与∠DOF相等吗?请说明理由.
(2)若∠DOF=![]() ∠BOE,求∠AOD的度数.
∠BOE,求∠AOD的度数.
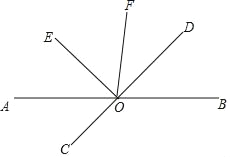
【答案】(1)∠BOD=∠DOF,理由详见解析;(2)∠AOD=150°.
【解析】
(1)由OE⊥OD知∠EOF+∠DOF=90°,∠AOE+∠BOD=90°,根据∠AOE=∠EOF即可得∠BOD=∠DOF;
(2)由∠DOF=![]() ∠BOE可∠DOF=x°,则∠BOE=4x°,∠BOD=x°,从而得∠DOE=∠BOE﹣∠BOD=3x°,根据∠DOE=90°可得x的值,继而根据∠AOD=180°﹣∠BOD即可得出答案.
∠BOE可∠DOF=x°,则∠BOE=4x°,∠BOD=x°,从而得∠DOE=∠BOE﹣∠BOD=3x°,根据∠DOE=90°可得x的值,继而根据∠AOD=180°﹣∠BOD即可得出答案.
解:(1)∠BOD=∠DOF,
∵OE⊥OD,
∴∠DOE=90°,
∴∠EOF+∠DOF=90°,∠AOE+∠BOD=90°,
∵OE平分∠AOF,
∴∠AOE=∠EOF,
∴∠BOD=∠DOF;
(2)∵∠DOF=![]() ∠BOE,
∠BOE,
∴设∠DOF=x°,则∠BOE=4x°,∠BOD=x°,
∴∠DOE=∠BOE﹣∠BOD=3x°,
∵∠DOE=90°,
∴3x=90,即x=30,
∴∠BOD=30°,
∴∠AOD=180°﹣∠BOD=150°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】“五四”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 12 |
B型 | 15 | 23 |
(1)设购进A型文具x只,销售利润为w元,求w与x的函数关系式?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
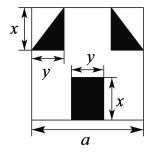
【题目】“囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形(阴影部分)和一个长方形(阴影部分)得到一个“囧”字图案,设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
(1)用含a、x、y的式子表示“囧”的面积;
(2)当a=12,x=7,y=4时,求该图形面积的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,OP是∠BOC的平分线.
(1)请写出图中所有∠EOC的补角 ____________________;
(2)如果∠POC:∠EOC=2:5.求∠BOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(4,5)、B(1,0)、C(4,0).
(1)画出△ABC关于y轴的对称图形△A1B1C1,并写出A1点的坐标;
(2)在y轴上求作一点P,使△PAB的周长最小,并求出点P的坐标及△PAB的周长最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
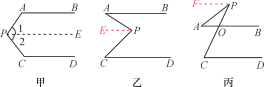
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣6x+c与x轴交于点A、B(5,0),与y轴交于点C(0,5),点P是抛物线上的动点,设点P的横坐标为t,连接PB、PC,PC与x轴交于点D,过点P作y轴的平行线交x轴于点H、交直线BC于点E.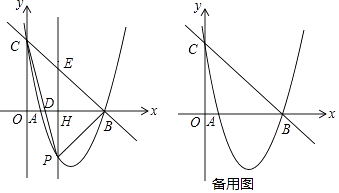
(1)求该抛物线所对应的函数解析式;
(2)若点P在第四象限,则△BPC的面积有值(填“最大”或“最小”),并求出其值;
(3)当t<5时,△BPE能否为等腰三角形?若能,请求出此时点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,动点P从点A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止;动点Q从A出发,以1cm/s的速度沿边AD匀速运动到D终止,若P、Q两点同时出发,运动时间为ts,△APQ的面积为Scm2 . S与t之间函数关系的图象如图2所示.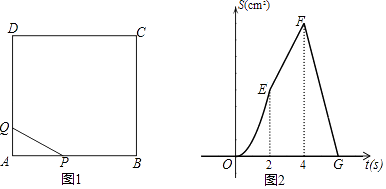
(1)求图2中线段FG所表示的函数关系式;
(2)当动点P在边AB运动的过程中,若以C、P、Q为顶点的三角形是等腰三角形,求t的值;
(3)是否存在这样的t,使PQ将正方形ABCD的面积恰好分成1:3的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com