
����Ŀ����ͼ��������y=ax2��6x+c��x�ύ�ڵ�A��B��5��0������y�ύ�ڵ�C��0��5������P���������ϵĶ��㣬���P�ĺ�����Ϊt������PB��PC��PC��x�ύ�ڵ�D������P��y���ƽ���߽�x���ڵ�H����ֱ��BC�ڵ�E��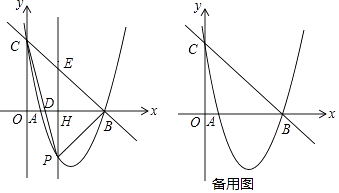
��1���������������Ӧ�ĺ�������ʽ��
��2������P�ڵ������ޣ����BPC�������ֵ��������С�������������ֵ��
��3����t��5ʱ����BPE�ܷ�Ϊ���������Σ����ܣ��������ʱ��P�����ꣻ�����ܣ���˵�����ɣ�
���𰸡�
��1��
�⣺��B��5��0����C��0��5����
��c=5��0=25a��30+c�����a=1��
�������߽���ʽΪy=x2��6x+5��
��2�����
��3��
�⣺���ڣ��������£�
�������֪P��t��t2��6t+5������H��t��0����E��t����t+5�����ҡ�BHEΪ����ֱ�������Σ�
��BE= ![]() BH=
BH= ![]() ��5��t����
��5��t����
�ߡ�BPEΪ���������Σ�
����PE=PB��BE=BP��BE=PE���������
�ٵ�PE=PBʱ�����ڡ�PEB=45�㣬
���PEBΪ����ֱ�������Σ���P��A�㴦����P��1��0�����������⣻
�ڵ�BE=BPʱ������PE��BH��
��HE=HP������E���P����x��Գƣ�
�ੁt+5+t2��6t+5=0�����t=2��t=5���������⣬��ȥ����
��P��2����3����
�۵�BE=PEʱ��
�ߡ�EHBΪ����ֱ�������Σ�
��BE= ![]() HB=
HB= ![]() ��5��t������PE=|��t2+5t|��
��5��t������PE=|��t2+5t|��
��|��t2+5t|= ![]() ��5��t�������t=��
��5��t�������t=�� ![]() ��t=5���������⣬��ȥ����
��t=5���������⣬��ȥ����
��P�� ![]() ��7��6
��7��6 ![]() ����
���� ![]() ��7+6
��7+6 ![]() ����
����
���Ͽ�֪�������������ĵ�P��������Ϊ��1��0����2����3���� ![]() ��7��6
��7��6 ![]() ����
���� ![]() ��7+6
��7+6 ![]() ����
����
����������2����B��5��0����C��0��5����
��ֱ��BC����ʽΪy=��x+5��
��P�ĺ�����Ϊt������PB��PC��PC��x�ύ�ڵ�D������P��y���ƽ���߽�x���ڵ�H����ֱ��BC�ڵ�E��
��P��t��t2��6t+5����E��t����t+5����
��PE=��t+5����t2��6t+5��=��t2+5t��
��S��PBC= ![]() OBPE=
OBPE= ![]() ��5����t2+5t��=��
��5����t2+5t��=�� ![]() ��t��
��t�� ![]() ��2+
��2+ ![]() ��
��
�ߩ� ![]() ��0��
��0��
��S��PBC�����ֵ�����ֵΪ ![]() ��
��
���Դ��ǣ����
�����㾫����������Ŀ����֪���������ö��κ��������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��


 �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ���ı���ABCD�У���A���B��������C=90�㣬DE��AB��EΪ���㣮����EDC=60�������B����A����ADE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
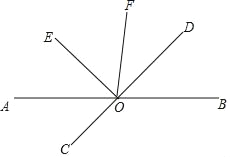
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OE��OD��OEƽ����AOF��
��1����BOD����DOF�������˵�����ɣ�
��2������DOF=![]() ��BOE������AOD�Ķ�����
��BOE������AOD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��վ���м��ֻ���1530�֣����ֻ���1150�֣�����һ�л���������ij���С��ɹ�A��B���ֲ�ͬ���ij���50�ڣ���֪��һ��A�ͳ������0.5 ��Ԫ����һ��B�ͳ���ķ���0.8��Ԫ.
(1)��֪���ֻ���35�ֺ����ֻ���15�ֿ�װ��һ��A�ͳ��ᣬ���ֻ���25�ֺ����ֻ���35�ֿ���װ��һ��B�ͳ��ᣬ�����A��B���ֳ���Ľ������м������䷽������һһд��.
(2)�ĸ������˷����٣������˷Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���»�����ɳ�ľ���ԼΪ200km��С������С�γ�����ʦ�����Ŵ���������»�ȥ��ɳ��С������ʦ��������20���ӣ��������ͬʱ���ﳤɳ����֪С�γ����ٶ��Ǵ�����ٶȵ�1.2������С�γ��ʹ�������ٶȸ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ��1������֪������ABC�У���BAC��90����AB=AC��ֱ��m������A��BD��ֱ��m, CE��ֱ��m,����ֱ�Ϊ��D��E.֤��:DE=BD+CE.
��2�� ��ͼ��2��������1���е�������Ϊ������ABC�У�AB=AC��D��A��E���㶼��ֱ��m��,��������BDA=��AEC=��BAC=![]() ,����
,����![]() Ϊ������ǻ�۽�.���ʽ���DE=BD+CE�Ƿ����?�����,�������֤��;��������,��˵������.
Ϊ������ǻ�۽�.���ʽ���DE=BD+CE�Ƿ����?�����,�������֤��;��������,��˵������.
��3����չ��Ӧ�ã���ͼ��3����D��E��D��A��E��������ֱ��m�ϵ������㣨D��A��E���㻥���غϣ�,��FΪ��BACƽ�����ϵ�һ��,����ABF����ACF��Ϊ�ȱ������Σ�����BD��CE,����BDA=��AEC=��BAC�����ж���DEF����״.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С���Ӽҵ���ѧУҪ����һ������С����С���ĵ�·�������ϻ�����������С����������·���ܵ���ѧУ����(����)
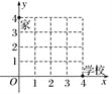
A. (0,4)��(0,0)��(4,0)
B. (0,4)��(4,4)��(4,0)
C. (0,4)��(3,4)��(4,2)��(4,0)
D. (0,4)��(1,4)��(1,1)��(4,1)��(4,0)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC �У��� AC��BC �Ĵ�ֱƽ���ߵĽ��� O ���ڱ� AB �ϣ����ABC ����״�ǣ� ��
A. �۽������� B. ֱ�������� C. ��������� D. ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ8��B��������һ�㣬��AB=22������P�ӵ�A��������ÿ��4����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt(t>0)�룮
(1)д�������ϵ�B��ʾ����____����P��ʾ����____���ú�t�Ĵ���ʽ��ʾ����
(2)������Q�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������������˶�������P��Qͬʱ�������ʵ�P�˶�������ʱ�ϵ�Q?����һԪһ�η��̽�Ӧ���⣩
(3)������Q�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������������˶�������P��Qͬʱ�������� ��ʱP��Q֮��ľ���ǡ�õ���2��ֱ��д���𰸣�
(4)˼���ڵ�P���˶������У���MΪAP���е㣬NΪPB���е�.�߶�MN�ij����Ƿ����仯�����仯����˵�����ɣ������䣬���㻭��ͼ�Σ�������߶�MN�ij�.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com