
【题目】阅读材料,解决下列问题:
材料一:对非负实数x“四舍五入”到个位的值记为![]() ,即:当n为非负整数时,如果
,即:当n为非负整数时,如果![]() ,则
,则![]() ;反之,当n为非负整数时,如果
;反之,当n为非负整数时,如果![]() ;则
;则![]() ,例如:
,例如:![]() ,
,![]() ,
,![]() ,
,![]()
材料二:平面直角坐标系中任意两点![]() ,
,![]() ,我们把
,我们把![]() 叫做
叫做![]() 、
、![]() 两点间的折线距离,并规定
两点间的折线距离,并规定![]() 若
若![]() 是一定点,
是一定点,![]() 是直线
是直线![]() 上的一动点,我们把
上的一动点,我们把![]() 的最小值叫做
的最小值叫做![]() 到直线
到直线![]() 的折线距离,例如:若
的折线距离,例如:若![]() ,
,![]() 则
则![]() .
.
![]() 如果
如果![]() ,写出实数x的取值范围;
,写出实数x的取值范围;![]() 已知点
已知点![]() ,点
,点![]() ,且
,且![]() ,求a的值.
,求a的值.
![]() 若m为满足
若m为满足![]() 的最大值,求点
的最大值,求点![]() 到直线
到直线![]() 的折线距离.
的折线距离.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.

(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当![]() 时,求
时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(列二元一次方程组解应用题)某公司共有3个一样规模的大餐厅和2个一样规模的小餐厅,经过测试同时开放2个大餐厅和1个小餐厅,可供300名员工就餐;同时开放1个大餐厅,1个小餐厅,可供170名员工就餐.
(1)请问1个大餐厅、1个小餐厅分别可供多少名员工就餐;
(2)如果3个大餐厅和2个小餐厅全部开放,那么能否供全体450名员工就餐?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在北京2008年第29届奥运会前夕,某超市在销售中发现:奥运会吉祥物— “福娃”平均每天可售出20套,每件盈利40元。为了迎接奥运会,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每套降价4元,那么平均每天就可多售出8套。要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 ![]() 的图象如图所示,有以下结论:①
的图象如图所示,有以下结论:① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④ ![]() ;⑤
;⑤ ![]() 其中所有正确结论的序号是( )
其中所有正确结论的序号是( )
A.①②
B.①③④
C.①②③⑤
D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
(1)边AC,AB,BC的长;
(2)点C到AB边的距离;
(3)求△ABC的面积.
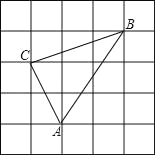
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为 ![]() ,宽为
,宽为 ![]() 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).

(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出 ![]() ,
,![]() ,
,![]() 之间的等量关系是 ;
之间的等量关系是 ;
(3)根据(2)中的结论,若 ![]() ,
,![]() ,则
,则 ![]() ;
;
(4)实际上我们可以用图形的面积表示许多恒等式,下面请你设计一个几何图形来表示恒等式![]() .在图形上把每一部分的面积标写清楚.
.在图形上把每一部分的面积标写清楚.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将平行四边形ABCD折叠,使顶点D恰落在AB边上的点M处,折痕为AN,那么下列说法不正确的是( )

A. MN∥BCB. MN=AMC. AN=BCD. BM=CN
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com