
【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.

(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当![]() 时,求
时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
【答案】(1)60,30;(2)![]() ;(3)采摘5千克或20千克草莓时,甲、乙两家采摘园的总费用相同.
;(3)采摘5千克或20千克草莓时,甲、乙两家采摘园的总费用相同.
【解析】
(1)根据单价=总价÷数量,即可解决问题;
(2)y乙与x的函数表达式结合图象利用待定系数法即可解决.
(3)根据图象可得y甲函数表达式,分别讨论x<10和x>10时,y甲=y乙,求出x的值即可.
(1)由图象可知:甲采摘园的门票是60元,
由y乙图象可知采摘草莓10千克的费用为300元,且超过10千克打折,
∴优惠前的草莓单价是每千克300÷10=30元,
故答案为:60,30;
(2)当![]() 时,设
时,设![]()
把点![]() ,
,![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]() ,
,
∴当![]() 时,
时,![]() ,
,
(3)![]()
当![]() 时,
时,![]()
![]() ,解得
,解得![]()
当![]() 时,
时,![]()
解得![]()
∴采摘5千克或20千克草莓时,甲、乙两家采摘园的总费用相同.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】已知某项工程由甲、乙两队合做12天可以完成,共需工程费用27720元.乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多250元.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应选择哪个工程队?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在边CD,BC上,且∠EAF=45°,BD分别交AE,AF于点M,N,以点A为圆心,AB长为半径画弧BD.下列结论:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④ ![]() 与EF相切;⑤EF∥MN.其中正确结论的个数是( )
与EF相切;⑤EF∥MN.其中正确结论的个数是( )
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=4,求平行四边形ADEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x﹣m)2﹣a(x﹣m)(a,m为常数,且a≠0).
(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;
(2)设该函数的图象与x轴的两个交点为A(x1 , 0),B(x2 , 0),且x12+x22=25,求m的值;
(3)设该函数的图象的顶点为C,与x轴交于A,B两点,且△ABC的面积为1,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.已知,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 在边
在边![]() 上,且
上,且![]() .
.

(1)如图![]() ,当
,当![]() 时,将
时,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() 的位置,连接
的位置,连接![]() ,
,
①求![]() 的度数;
的度数;
②求证:![]() ;
;
(2)如图![]() ,当
,当![]() 时,猜想
时,猜想![]() 、
、![]() 、
、![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)如图![]() ,当
,当![]() ,
,![]() ,
,![]() 时,请直接写出
时,请直接写出![]() 的长为________.
的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2 , 以AD2为一边,做第二个菱形AB2C2D2 , 使∠B2=60°;作AD3⊥B2C2于点D3 , 以AD3为一边做第三个菱形AB3C3D3 , 使∠B3=60°…依此类推,这样做的第n个菱形ABnCnDn的边ADn的长是 . 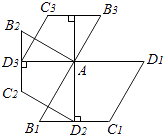
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你补全证明过程:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:EF∥CD

证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=90°,∠ACB=90°①( )
∴∠DGB=∠ACB ②( )
∴DG∥AC ③( )
∴∠2= ④________ ⑤( )
又∠1=∠2 ⑥( )
∴∠1=∠DCA ⑦( )
∴EF∥CD ⑧( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解决下列问题:
材料一:对非负实数x“四舍五入”到个位的值记为![]() ,即:当n为非负整数时,如果
,即:当n为非负整数时,如果![]() ,则
,则![]() ;反之,当n为非负整数时,如果
;反之,当n为非负整数时,如果![]() ;则
;则![]() ,例如:
,例如:![]() ,
,![]() ,
,![]() ,
,![]()
材料二:平面直角坐标系中任意两点![]() ,
,![]() ,我们把
,我们把![]() 叫做
叫做![]() 、
、![]() 两点间的折线距离,并规定
两点间的折线距离,并规定![]() 若
若![]() 是一定点,
是一定点,![]() 是直线
是直线![]() 上的一动点,我们把
上的一动点,我们把![]() 的最小值叫做
的最小值叫做![]() 到直线
到直线![]() 的折线距离,例如:若
的折线距离,例如:若![]() ,
,![]() 则
则![]() .
.
![]() 如果
如果![]() ,写出实数x的取值范围;
,写出实数x的取值范围;![]() 已知点
已知点![]() ,点
,点![]() ,且
,且![]() ,求a的值.
,求a的值.
![]() 若m为满足
若m为满足![]() 的最大值,求点
的最大值,求点![]() 到直线
到直线![]() 的折线距离.
的折线距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com