
����Ŀ����ͼ1��һ����Ϊ ![]() ����Ϊ
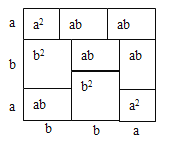
����Ϊ ![]() �ij����Σ���ͼ�������ü���ƽ���ֳ��Ŀ�С�����Σ�Ȼ�����Ŀ�С������ƴ�ɵ�һ���������������Σ���ͼ2����
�ij����Σ���ͼ�������ü���ƽ���ֳ��Ŀ�С�����Σ�Ȼ�����Ŀ�С������ƴ�ɵ�һ���������������Σ���ͼ2����

��1��ͼ2�е���Ӱ���ֵ����Ϊ ��
��2���۲�ͼ2����д�� ![]() ��
��![]() ��
��![]() ֮��ĵ�����ϵ�� ��
֮��ĵ�����ϵ�� ��
��3�����ݣ�2���еĽ��ۣ��� ![]() ��
��![]() ����
���� ![]() ��
��
��4��ʵ�������ǿ�����ͼ�ε������ʾ������ʽ�������������һ������ͼ������ʾ���ʽ![]() ����ͼ���ϰ�ÿһ���ֵ������д�����
����ͼ���ϰ�ÿһ���ֵ������д�����
���𰸡���1��![]() ����2��
����2��![]() ����3����5����4���������
����3����5����4���������
��������
��1����ʾ����Ӱ���������εı߳���Ȼ����������ε������ʽ��ʽ���ɣ�
��2�����ݴ������ε������ȥС�����ε���������ĸ�С�����ε������ʽ���ɣ�
��3������x-y��2����Ϊ��x+y��2��4xy���ٴ�����ֵ���ɣ�
��4������֪�ĺ��ʽ��������Ӧ��ͼ�Σ���ͼ��ʾ��
�⣺��1����Ӱ����Ϊһ�������Σ���߳�Ϊb-a��
���������![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2���������������![]()
С���������Ϊ��![]() =
=![]() ��
��
�����ĸ������ε����Ϊ��![]() ��
��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��3���ɣ�2��֪��![]() ��
��
��![]() ��
��
��![]() =
=![]() ��
��
�ʴ�Ϊ����5��
��4�����ϵ�ʽ![]() ��ͼ����ͼ��ʾ��
��ͼ����ͼ��ʾ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������AB1C1D1�ı߳�Ϊ1����B1=60�㣻��AD2��B1C1�ڵ�D2 �� ��AD2Ϊһ�ߣ����ڶ�������AB2C2D2 �� ʹ��B2=60�㣻��AD3��B2C2�ڵ�D3 �� ��AD3Ϊһ��������������AB3C3D3 �� ʹ��B3=60�㡭�������ƣ��������ĵ�n������ABnCnDn�ı�ADn�ij��� �� 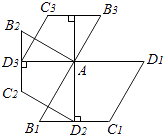
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�����������⣺
����һ���ԷǸ�ʵ��x����������������λ��ֵ��Ϊ![]() ��������nΪ�Ǹ�����ʱ�����
��������nΪ�Ǹ�����ʱ�����![]() ����
����![]() ����֮����nΪ�Ǹ�����ʱ�����
����֮����nΪ�Ǹ�����ʱ�����![]() ����
����![]() �����磺
�����磺![]() ��
��![]() ��
��![]() ��
��![]()
���϶���ƽ��ֱ������ϵ����������![]() ��
��![]() �����ǰ�
�����ǰ�![]() ����
����![]() ��
��![]() ���������߾��룬���涨
���������߾��룬���涨![]() ��
��![]() ��һ���㣬
��һ���㣬![]() ��ֱ��
��ֱ��![]() �ϵ�һ���㣬���ǰ�
�ϵ�һ���㣬���ǰ�![]() ����Сֵ����
����Сֵ����![]() ��ֱ��
��ֱ��![]() �����߾��룬���磺��
�����߾��룬���磺��![]() ��
��![]() ��
��![]() ��
��
![]() ���
���![]() ��д��ʵ��x��ȡֵ��Χ��
��д��ʵ��x��ȡֵ��Χ��![]() ��֪��
��֪��![]() ����
����![]() ����
����![]() ����a��ֵ��
����a��ֵ��
![]() ��m����
��mΪ����![]() �����ֵ�����
�����ֵ�����![]() ��ֱ��
��ֱ��![]() �����߾��룮
�����߾��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=��![]() x+8��x�ᡢy��ֱ��ڵ�A�͵�B��M��OB�ϵ�һ�㣬������ABM��AM�۵�����Bǡ������x���ϵĵ�B��������ֱ��AM�ĺ�������ʽ�ǣ�������
x+8��x�ᡢy��ֱ��ڵ�A�͵�B��M��OB�ϵ�һ�㣬������ABM��AM�۵�����Bǡ������x���ϵĵ�B��������ֱ��AM�ĺ�������ʽ�ǣ�������

A. y=��![]() x+8 B. y=��
x+8 B. y=��![]() x+8 C. y=��
x+8 C. y=��![]() x+3 D. y=��
x+3 D. y=��![]() x+3
x+3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������꼶��һ����������У���ͼ��Ա������Ͷ������֪�����ʱ������ ![]() m������Ȧ���ĵ�ˮƽ����Ϊ7m��������ֺ�ˮƽ����Ϊ4mʱ�������߶�4m�����������еĹ켣Ϊ�����ߣ���Ȧ�����3m��
m������Ȧ���ĵ�ˮƽ����Ϊ7m��������ֺ�ˮƽ����Ϊ4mʱ�������߶�4m�����������еĹ켣Ϊ�����ߣ���Ȧ�����3m��
��1��������ͼ��ʾ��ƽ��ֱ������ϵ���������ߵĽ���ʽ���жϴ����ܷ�ȷͶ�У�
��2����ʱ�����Է���Ա���ڼ�ǰ��1m�������ñ���أ���֪�ҵ��������Ϊ3.1m����ô���ܷ��óɹ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��AOB�͡�COD�����߷ֱ��ഹֱ���ҡ�COD�ȡ�AOB��3����60�㣬���COD�Ķ���Ϊ_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���A����BCD��90�㣬BC��DC���ӳ�AD��E��ʹDE��AB.
��1����֤����ABC����EDC��
��2����֤����ABC�ա�EDC.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����գ��������˵������
��ͼ����A��O��B��ͬһ��ֱ���ϣ� OD��OE�ֱ�ƽ�֡�AOC�͡�BOC��

��1�����DOE�Ķ�����
��2�������COD=65�������AOE�Ķ���.
�⣺��1����ͼ����ΪOD�ǡ�AOC��ƽ���ߣ�
���ԡ�COD =![]() ��AOC��
��AOC��
��ΪOE�ǡ�BOC ��ƽ���ߣ�
���� =![]() ��BOC��
��BOC��
���ԡ�DOE=��COD+ =![]() ����AOC+��BOC��=
����AOC+��BOC��=![]() ��AOB= ����
��AOB= ����
��2���ɣ�1����֪��BOE=��COE = ����COD= ��.
���ԡ�AOE= ����BOE = ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com