
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
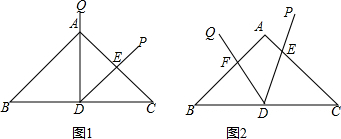
 等边△ABC高为7$\sqrt{3}$,边长为14.BD为AC边上高,P是BD上的动点,且E是BC上-点,BE=CE,则△PEC的周长最小值为7$\sqrt{3}$+7.
等边△ABC高为7$\sqrt{3}$,边长为14.BD为AC边上高,P是BD上的动点,且E是BC上-点,BE=CE,则△PEC的周长最小值为7$\sqrt{3}$+7.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳老河口九年级3月月考数学试卷(解析版) 题型:判断题
某产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点在原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额-生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
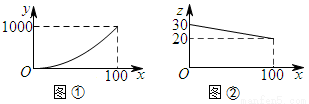
查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳老河口九年级3月月考数学试卷(解析版) 题型:单选题
若顺次连接四边形ABCD各边中点所得到的四边形是矩形,则四边形ABCD一定是( )
A. 菱形 B. 对角线互相垂直的四边形
C. 矩形 D. 对角线相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com