练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．等边△ABC高为7$\sqrt{3}$，边长为14．BD为AC边上高，P是BD上的动点，且E是BC上-点，BE=CE，则△PEC的周长最小值为7$\sqrt{3}$+7．

    分析 因为CE=7是定值，要求△PEC的周长最小值，只要求得EP+CP的最小值即可，这就需考虑通过作辅助线转化EP，CP的值，从而找出其最小值求解．

    解答 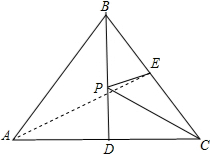解：连接AE，与BD交于点P．
    ∵BD为AC边上高，
    ∴AD=DC，
    ∴BD是AC的垂直平分线，
    ∴A、C关于BD对称，
    ∴AP=CP，
    ∴PE+PC=PE+PA=AE，
    ∴AE就是EP+CP的最小值．
    ∵BE=CE，
    ∴AE是等边△ABC的高，
    ∴AE=7$\sqrt{3}$，
    ∴△PEC的周长最小值为PE+PC+EC=AE+CE=7$\sqrt{3}$+7．
    故答案为7$\sqrt{3}$+7．

    点评 考查等边三角形的性质和轴对称-最短路线问题，熟练掌握和运用等边三角形的性质以及轴对称的性质是本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．计算：$\sqrt{12}$-4$\sqrt{\frac{1}{2}}$-tan60°+|$\sqrt{3}$-2|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．请估计$\sqrt{10}-1$的值在（　　）
    A．1与2之间B．2与3之间C．3与4之间D．4与5之间

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如图，△ABC中，∠C=90°，若CD⊥AB于D，且BD=4，AD=9，则CD=6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知，等腰梯形ABCD中，AD∥BC，∠B=∠BCD=45°，AD=3，BC=9，点P是对角线AC上的一个动点，且∠APE=∠B，PE分别交射线AD和射线CD于点E和点G；

    （1）如图1，当点E、D重合时，求AP的长；
    （1）如图2，当点E在AD的延长线上时，设AP=x，DE=y，求y关于x的函数解析式，并写出它的定义域；
    （3）当线段DG=$\sqrt{2}$时，求AE的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列式子中，字母x的取值范围是x＞2的式子是（　　）
    A．y=$\sqrt{x-2}$B．y=$\frac{1}{\sqrt{x-2}}$C．y=$\sqrt{2x-1}$D．y=$\frac{1}{\sqrt{2x-1}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知a，b，c为一个三角形的三边长，化简$\sqrt{（a+b+c）^{2}}$+$\sqrt{（a+b-c）^{2}}$-|b-c-a|+$\sqrt{（b+c-a）^{2}}$．

    查看答案和解析>>

    科目：初中数学 来源：2017届湖北省襄阳老河口九年级3月月考数学试卷（解析版） 题型：判断题

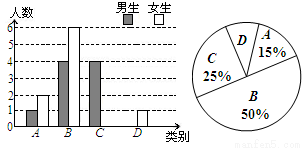
    本学期开学初，李老师为了了解所教班级学生假期自学任务完成情况，对部分学生进行了抽查，抽查结果分成四类，A：特别好；B：好；C：一般；D：较差；并将抽査结果绘制成以下两幅不完整的统计图（如图所示），请你根据统计图解答下列问题：

    （1）李老师一共抽查了 名同学，其中女生有 名；

    （2）将条形统计图补充完整；

    （3）李老师想从被抽查的A类和D类学生中分别选取一位进行“一帮一”互助，所选的两位同学恰好是一男一女的概率是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

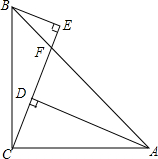    5．如图，AD=CE=24，BC=25，∠BCE=∠CAD，BE∥AD，BF：AF=7：24，给出下列结论：①∠E=90°；②∠BCA=90°；③∠BAC=45°；④AB=25$\sqrt{3}$．其中正确的结论有①②③．（把所有正确结论序号都填在横线上）

    查看答案和解析>>

    同步练习册答案