
【题目】定义:给定两个不等式组![]() 和
和![]() ,若不等式组
,若不等式组![]() 的任意一个解,都是不等式组
的任意一个解,都是不等式组![]() 的一个解,则称不等式组
的一个解,则称不等式组![]() 为不等式组
为不等式组![]() 的“子集”。例如:不等式组:
的“子集”。例如:不等式组:![]() 是:
是:![]() 的“子集”。
的“子集”。
(1)若不等式组:![]() ,
,![]() ,则其中不等式组 是不等式组
,则其中不等式组 是不等式组![]() 的“子集”(填
的“子集”(填![]() 或
或![]() );
);
(2)若关于![]() 的不等式组
的不等式组![]() 是不等式组
是不等式组![]() 的“子集”,则
的“子集”,则![]() 的取值范围是 ;
的取值范围是 ;
(3)已知![]() ,
,![]() ,
,![]() ,
,![]() 为互不相等的整数,其中
为互不相等的整数,其中![]() ,
,![]() ,下列三个不等式组:
,下列三个不等式组:![]() ,
,![]() ,
,![]() 满足:
满足:![]() 是
是![]() 的“子集”且
的“子集”且![]() 是
是![]() 的“子集”,求
的“子集”,求![]() 的值;
的值;
(4)已知不等式组![]() 有解,且是不等式组
有解,且是不等式组![]() 的“子集”,则满足条件的有序整数对
的“子集”,则满足条件的有序整数对![]() 共有多少个?
共有多少个?
【答案】(1)A;(2)a≥2;(3)-4;(4)10.
【解析】
(1)先分别求出不等组A,B的解集,再根据不等式组子集的定义进行判断即可.
(2)先求出不等式组![]() 的解集为x>2,再根不等组子集的定义,可得不等式组
的解集为x>2,再根不等组子集的定义,可得不等式组![]() 的解集在x>2的内部,故a≥2.
的解集在x>2的内部,故a≥2.
(3)先根据子集的定义求出a=3,b=4,c=2,d=5.代入式子求解即可.
(4)先根据子集的定义确定出m,n的取值范围,再由它均为整数,从而确定出有序整数对![]() 共有10个.
共有10个.
解:(1)∵![]() ,
,
∴A的解集为:3<x<6.
∵![]() ,
,
∴B的解集为x>1.
∵![]() ,
,
∴M的解集为x>2.
∴A是M的子集.
故答案为:A.
(2)∵不等式组![]() 的解集为x>2,且关于
的解集为x>2,且关于![]() 的不等式组
的不等式组![]() 是不等式组
是不等式组![]() 的“子集”,
的“子集”,
∴![]() 的取值范围是a≥2.
的取值范围是a≥2.
故答案为:a≥2.
(3)∵![]() 是
是![]() 的“子集”,
的“子集”,
∴c≤a≤b≤d.
∵![]() ,
,![]() ,
,![]() ,
,![]() 为互不相等的整数,其中
为互不相等的整数,其中![]() ,
,![]() ,
,
∴c<![]() <d.
<d.
∵![]() 是
是![]() 的“子集”,
的“子集”,
∴1< c<![]() <d<6.
<d<6.
∴a=3,b=4,c=2,d=5.
∴![]() =3-4+2-5=-4.
=3-4+2-5=-4.
(4)∵不等式组![]() 有解,
有解,
∴不等式组M的解集为![]() ≤x≤
≤x≤![]() ,
,
∵不等式组![]() 是不等式组
是不等式组![]() 的“子集”,
的“子集”,
∴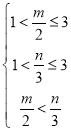 ,
,
解得: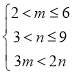 ,
,
∵m,n为整数,
∴足条件的有序整数对![]() 共有10个,它们分别是(3,5)、(3,6)、(3,7)、(3,8)、(3,9)、(4,7)、(4,8)、(4,9)、(5,8)、(5,9).
共有10个,它们分别是(3,5)、(3,6)、(3,7)、(3,8)、(3,9)、(4,7)、(4,8)、(4,9)、(5,8)、(5,9).


科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为直线AB上一点,过点O作射线OC,使![]() .将一个含
.将一个含![]() 角的直角三角板OMN的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边ON,MN都在直线AB的下方.
角的直角三角板OMN的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边ON,MN都在直线AB的下方.

(1)将图1中的三角板OMN绕着点O逆时针旋转![]() ,如图2所示,请问OM是否平分
,如图2所示,请问OM是否平分![]() ?请说明理由;
?请说明理由;
(2)将图2中的三角板OMN绕点O逆时针继续旋转到图3的位置所示,使得ON在![]() 的内部,请探究
的内部,请探究![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)将图1中的三角板OMN绕点O按每秒![]() 的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直角边ON所在直线恰好平分锐角
的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直角边ON所在直线恰好平分锐角![]() ,则t的值为________(直接写出结果).
,则t的值为________(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第一届中非经贸博览会于![]() 年
年![]() 月
月![]() 日至
日至![]() 日在长沙举办,为了抓住商机,某服装店决定购进甲、乙两种文化衫进行销售,若购进甲种文化衫
日在长沙举办,为了抓住商机,某服装店决定购进甲、乙两种文化衫进行销售,若购进甲种文化衫![]() 件,乙种文化衫
件,乙种文化衫![]() 件,需要
件,需要![]() 元;若购进甲种文化衫
元;若购进甲种文化衫![]() 件,乙种文化衫
件,乙种文化衫![]() 件,需要
件,需要![]() 元.
元.
(1)求购进甲、乙两种文化衫每件各需多少元?
(2)若该服装店决定用不超过![]() 元的资金购进这两种服装共
元的资金购进这两种服装共![]() 件,且用于购买甲种文化衫的资金不低于购买乙种文化衫的资金,那么该商店共有哪几种进货方案?
件,且用于购买甲种文化衫的资金不低于购买乙种文化衫的资金,那么该商店共有哪几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-![]() x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
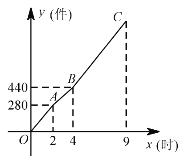
【题目】某玩具厂加工了一批玩具“六一”捐赠给儿童福利院,甲、乙两车间同时开始加工这批玩具,加工一段时间后,甲车间的设备出现故障停产一段时间,乙车间继续加工,甲维修好设备后继续按照原来的工作效率加工,从工作开始到加工完这批玩具乙车间工作![]() 小时,甲、乙两车间加工玩具的总数量
小时,甲、乙两车间加工玩具的总数量 ![]() (件)与加工时间
(件)与加工时间 ![]() (时)之间的函数图象如图所示.
(时)之间的函数图象如图所示.
(1)求乙车间每小时加工玩具的数量.
(2)求甲车间维修完设备后,![]() 与
与 ![]() 之间的函数关系式.
之间的函数关系式.
(3)何时能加工一半?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你认真阅读下面的小探究系列,完成所提出的问题.
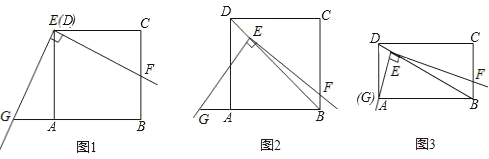
(1)如图1,将角尺放在正方形ABCD上,使角尺的直角顶点E与正方形ABCD的顶点D重合,角尺的一边交CB于点F,将另一边交BA的延长线于点G.求证:EF=EG.
(2)如图2,移动角尺,使角尺的顶点E始终在正方形ABCD的对角线BD上,其余条件不变,请你思考后直接回答EF和EG的数量关系:EF EG(用“=”或“≠”填空)
(3)运用(1)(2)解答中所积累的活动经验和数学知识,完成下题:如图3,将(2)中的“正方形ABCD”改成“矩形ABCD”,使角尺的一边经过点A(即点G、A重合),其余条件不变,若AB=4,BC=3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
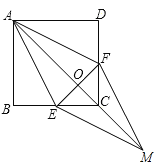
【题目】已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:BE=DF;
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com