
【题目】已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:BE=DF;
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
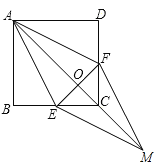
【答案】(1)见解析;(2)四边形AEMF是菱形,见解析.
【解析】
(1)求简单的线段相等,可证线段所在的三角形全等,即证△ABE≌△ADF;
(2)由于四边形ABCD是正方形,易得∠ECO=∠FCO=45°,BC=CD;联立(1)的结论,可证得EC=CF,根据等腰三角形三线合一的性质可证得OC(即AM)垂直平分EF;已知OA=OM,则EF、AM互相平分,再根据一组邻边相等的平行四边形是菱形,即可判定四边形AEMF是菱形.
解:(1)∵ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
又∵AE = AF,
∴![]() (HL),
(HL),
∴BE = DF;
(2)四边形AEMF是菱形,理由为:
证明:∵四边形ABCD是正方形,
∴∠BCA=∠DCA=45°(正方形的对角线平分一组对角),
BC=DC(正方形四条边相等),
∵BE=DF(已证),
∴BC-BE=DC-DF(等式的性质),
即CE=CF,
在△COE和△COF中,
 ,
,
∴△COE≌△COF(SAS),
∴OE=OF,又OM=OA,
∴四边形AEMF是平行四边形(对角线互相平分的四边形是平行四边形),
∵AE=AF,
∴平行四边形AEMF是菱形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】定义:给定两个不等式组![]() 和
和![]() ,若不等式组
,若不等式组![]() 的任意一个解,都是不等式组
的任意一个解,都是不等式组![]() 的一个解,则称不等式组
的一个解,则称不等式组![]() 为不等式组
为不等式组![]() 的“子集”。例如:不等式组:
的“子集”。例如:不等式组:![]() 是:
是:![]() 的“子集”。
的“子集”。
(1)若不等式组:![]() ,
,![]() ,则其中不等式组 是不等式组
,则其中不等式组 是不等式组![]() 的“子集”(填
的“子集”(填![]() 或
或![]() );
);
(2)若关于![]() 的不等式组
的不等式组![]() 是不等式组
是不等式组![]() 的“子集”,则
的“子集”,则![]() 的取值范围是 ;
的取值范围是 ;
(3)已知![]() ,
,![]() ,
,![]() ,
,![]() 为互不相等的整数,其中
为互不相等的整数,其中![]() ,
,![]() ,下列三个不等式组:
,下列三个不等式组:![]() ,
,![]() ,
,![]() 满足:
满足:![]() 是
是![]() 的“子集”且
的“子集”且![]() 是
是![]() 的“子集”,求
的“子集”,求![]() 的值;
的值;
(4)已知不等式组![]() 有解,且是不等式组
有解,且是不等式组![]() 的“子集”,则满足条件的有序整数对
的“子集”,则满足条件的有序整数对![]() 共有多少个?
共有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李林想了解班上同学是否具有阅读习惯及分享意识,于是设计了一份调查问卷:

李林对班上![]() 位同学进行了调查,收集调查结果如下:
位同学进行了调查,收集调查结果如下:
问题1的调查结果
选项 |
|
|
|
人数 |
|
|
|
问题2的调查结果
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() 请在下图中将问题1的调查结果用条形统计图表示出来:
请在下图中将问题1的调查结果用条形统计图表示出来:

![]() 请用下面的统计表整理问题2的调查结果:
请用下面的统计表整理问题2的调查结果:
选项 | 划记 | 人数 | 百分比 |
| |||
| |||
| |||
合计 |
![]() 根据调查结果,你认为班上同学在阅读习惯及分享意识方面做得怎么样?
根据调查结果,你认为班上同学在阅读习惯及分享意识方面做得怎么样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试解答下列问题:
(1)在图1我们称之为“8字形”,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数是 个;
(3) 在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试写出∠B与∠P、∠D之间数量关系 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图(2),∠BDC的平分线分别交AC,BC于点E,F,求∠CEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”。应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F. 若AB=6,BC=![]() ,则FD的长为( )
,则FD的长为( )
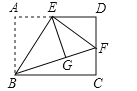
A. 2B. 4C. 6D. 23
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是计算机中的一种益智小游戏“扫雷”的画面,在一个![]() 的小方格的正方形 雷区中,随机埋藏着
的小方格的正方形 雷区中,随机埋藏着![]() 颗地雷,每个小方格内最多只能埋藏
颗地雷,每个小方格内最多只能埋藏![]() 颗地雷。小红在游戏开始时首先随机的点击一个方格,该方格中出现了数字“
颗地雷。小红在游戏开始时首先随机的点击一个方格,该方格中出现了数字“![]() ”,其意义表示该格的外围区域(图中阴影部分,记为
”,其意义表示该格的外围区域(图中阴影部分,记为![]() 区域)有
区域)有![]() 颗地雷;接着小红又点击了左上角第一个方格,出现了数字“
颗地雷;接着小红又点击了左上角第一个方格,出现了数字“![]() ”,其外围区域(图中阴影)记为
”,其外围区域(图中阴影)记为![]() 区域;
区域;![]() 区域与
区域与![]() 区域以及出现数字“
区域以及出现数字“![]() ”和“
”和“![]() ”两格以外的部分记为
”两格以外的部分记为![]() 区域。请分别计算出
区域。请分别计算出![]() 区、
区、![]() 区、
区、![]() 区点中地雷的概率,那么她应点击
区点中地雷的概率,那么她应点击![]() 、
、![]() 、
、![]() 中的哪个区域?
中的哪个区域?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com