
【题目】如图,在□ABCD中,BC=2AB,M是AD的中点,CE⊥AB,垂足为E,求证:∠DME=3∠AEM.

【答案】证明见解析
【解析】
设CM与BA相交于点N,证明△CMD≌△NMA ,得到AN=CD,∠ANM=∠MCD,根据BC=2AB,得到BC=BN,根据等边对等角有∠BNC=∠BCN,根据三角形外角的性质得到∠DME=∠AEM+∠EAM=∠AEM+2∠BNC,根据直角三角形斜边的中线等于斜边的一半得到EM=MN则∠AEM=∠BNC,即可证明.
如图,设CM与BA相交于点N
∵四边形ABCD是平行四边形,M是AD的中点
∴△CMD≌△NMA
∴AN=CD,
∠ANM=∠MCD,
又BC=2AB
∴BC=BN
即∠BNC=∠BCN
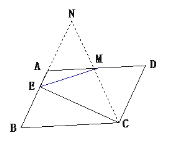
又∠EMD是△AEM的外角,∠EAM=∠BCD
∴∠DME=∠AEM+∠EAM
=∠AEM+∠BCD
=∠AEM+∠BCN+∠DCM
=∠AEM+∠BNC+∠DCM
=∠AEM+2∠BNC
又CE⊥AB
∴EM是Rt△CEN中斜边上的中线
∴EM=MN
∴∠AEM=∠BNC
∴∠DME=3∠AEM


科目:初中数学 来源: 题型:
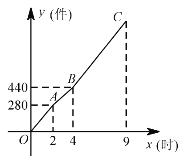
【题目】某玩具厂加工了一批玩具“六一”捐赠给儿童福利院,甲、乙两车间同时开始加工这批玩具,加工一段时间后,甲车间的设备出现故障停产一段时间,乙车间继续加工,甲维修好设备后继续按照原来的工作效率加工,从工作开始到加工完这批玩具乙车间工作![]() 小时,甲、乙两车间加工玩具的总数量
小时,甲、乙两车间加工玩具的总数量 ![]() (件)与加工时间
(件)与加工时间 ![]() (时)之间的函数图象如图所示.
(时)之间的函数图象如图所示.
(1)求乙车间每小时加工玩具的数量.
(2)求甲车间维修完设备后,![]() 与
与 ![]() 之间的函数关系式.
之间的函数关系式.
(3)何时能加工一半?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x、y的二元一次方程组![]() 的解都为正数.
的解都为正数.
(1)求a的取值范围;
(2)化简|a+1|﹣|a﹣1|;
(3)若上述二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
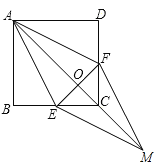
【题目】已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:BE=DF;
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格相同).若购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元,购买
元,购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元.
元.
![]() 求篮球、足球的单价各是多少元;
求篮球、足球的单价各是多少元;
![]() 根据学校实际需要,需一次性购买篮球和足球共
根据学校实际需要,需一次性购买篮球和足球共![]() 个.要求购买篮球和足球的总费用不超过
个.要求购买篮球和足球的总费用不超过![]() 元,则该校最多可以购买多少个篮球?
元,则该校最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了统计知识后,数学老师请数学兴趣小组的同学就本班同学的上学方式进行了一次调查统计.如图甲乙是数学兴趣小组的同学们通过手机和整理数据后,绘制的两幅不完整的统计图.
请你根据图中提供的信息,解答一下的问题:
(1)在扇形统计图中,计算出“步行”部分所应对的圆心角的度数.
(2)请问该班共有多少名学生?
(3)在图中将表示“乘车”的部分补充完整.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要开展校园艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下两幅不完整的统计图.
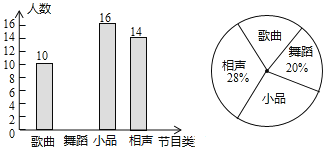
请根据图中信息,回答下列问题:
(1)本次共调查了_________名学生.
(2)在扇形统计图中,“歌曲”所在扇形的圆心角等于_________度.
(3)补全条形统计图(并标注频数).
(4)根据以上统计分析,估计该校2000名学生中最喜爱小品的人数约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明从P点出发,沿北偏东60°方向行驶到达A处,接着向正南方向行驶100(![]() +1)米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少米?
+1)米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com