
| 3 |
| 4 |
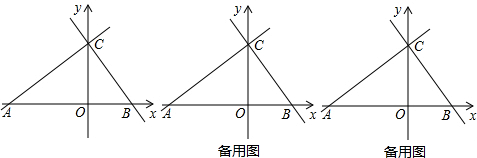
| 3 |
| 4 |
| OC |
| OA |
| OB |
| OC |
| 15 |
| 2 |
| 15 |
| 2 |
| 5 |
| 2 |
| 2 |
5
| ||
| 4 |
| ||
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
 解:(1)∵y=
解:(1)∵y=| 3 |
| 4 |
| OC |
| OA |
| OB |
| OC |
| 6 |
| 8 |
| a |
| 6 |
| 9 |
| 2 |
| 9 |
| 2 |
|
|
| 4 |
| 3 |
| 9 |
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |
| 5 |
| 2 |
| 2 |
| 5 |
| 2 |
5
| ||
| 4 |
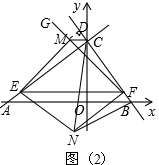
5
| ||
| 4 |
| ||
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
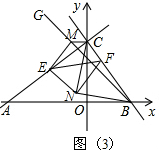
| 5 |
| 4 |


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
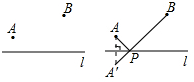 已知直线l的同侧有A,B两点(图1),要在直线l上确定一点P,使PA+PB的值最小.小明同学的做法如图2:①作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′P+PB=A′B,由“两点之间,线段最短”可知,点P即为所求的点.请问小明同学的做法是否正确?说明理由.
已知直线l的同侧有A,B两点(图1),要在直线l上确定一点P,使PA+PB的值最小.小明同学的做法如图2:①作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′P+PB=A′B,由“两点之间,线段最短”可知,点P即为所求的点.请问小明同学的做法是否正确?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)画出图中△ABC的高AD(标注出点D的位置);画出图中△ABC的角平分线AE(标注出点E的位置);
(1)画出图中△ABC的高AD(标注出点D的位置);画出图中△ABC的角平分线AE(标注出点E的位置);查看答案和解析>>
科目:初中数学 来源: 题型:
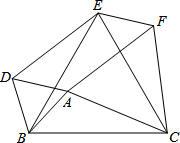 如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.
如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com