练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，AB=AC，∠BAC=120°，AE=BE，D为EC中点．

    （1）求∠CAE的度数；

    （2）求证：△ADE是等边三角形．

    【答案】（1）90°；（2）证明见解析

    【解析】

    试题分析：（1）根据等腰三角形两底角相等求出∠B=30°，∠BAE=∠B=30°，即可得出结果；

    （2）根据直角三角形斜边上的中线性质得出AD=EC=ED=DC，得出∠DAC=∠C=30°，因此∠EAD=60°，即可得出结论．

    （1）解：∵AB=AC，∠BAC=120°，

    ∴∠B=×（180°-120°）=30°，

    ∵AE=BE，

    ∴∠BAE=∠B=30°，

    ∴∠CAE=120°-30°=90°；

    （2）证明：∵∠CAE=90°，D是EC的中点，

    ∴AD=EC=ED=DC，

    ∴∠DAC=∠C=30°，

    ∴∠EAD=60°，

    ∴△ADE是等边三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某县为大力推进义务教育均衡发展，加强学校标准化建设，计划用三年时间对全县学校的设施和设备进行全面改造和更新．2014年县政府已投资5亿元人民币，若每年投资的增长率相同，预计2016年投资7.2亿元人民币，那么每年投资的增长率为（ ）

    A. 20% B. 40% C. －220% D. 20%

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若3xmy3与-x2yn是同类项，则（-m）n等于（ ）
    A.6
    B.-6
    C.8
    D.-8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

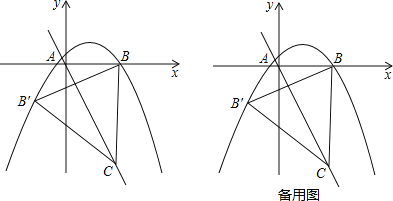
    【题目】综合与探究：如图，抛物线y=﹣x2+bx+c与x轴交于A（﹣1，0），B（5，0）两点，过点B作线段BC⊥x轴，交直线y=﹣2x于点C．

    （1）求该抛物线的解析式；

    （2）求点B关于直线y=﹣2x的对称点B′的坐标，判定点B′是否在抛物线上，并说明理由；

    （3）点P是抛物线上一动点，过点P作y轴的平行线，交线段B′C于点D，是否存在这样的点P，使四边形PBCD是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

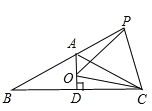
    【题目】如图，在等腰三角形ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，下面的结论:①∠APO+∠DCO=30°；②△OPC是等边三角形；③AC=AO+AP；④．其中所有正确结论的序号为 ( )

    A.①②③ B．①②④ C．①③④ D．①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】81的平方根为（ ）

    A. 9 B. ±9 C. －9 D. ±3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正三角形、正方形、等腰直角三角形、平行四边形中，既是轴对称图形又是中心对称图形的是（ ）
    A.正三角形
    B.正方形
    C.等腰直角三角形
    D.平行四边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一次课堂练习，小璇同学做了如下4道因式分解题，你认为小璇做得不正确的一题是(　　)

    A. a3－a＝a(a2－1)

    B. m2－2mn＋n2＝(m－n)2

    C. x2y－xy2＝xy(x－y)

    D. x2－y2＝(x－y)(x＋y)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个角的度数比它的余角的度数大20°，则这个角的度数是（　　）
    A.20°
    B.35°
    C.45°
    D.55°

    查看答案和解析>>

    同步练习册答案