
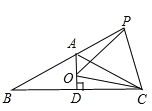
【题目】如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④![]() .其中所有正确结论的序号为 ( )
.其中所有正确结论的序号为 ( )
A.①②③ B.①②④ C.①③④ D.①②③④
【答案】D.
【解析】
试题解析:连接OB,
∵AB=AC,AD⊥BC,
∴BD=CD,∠BAD=![]() ∠BAC=
∠BAC=![]() ×120°=60°,
×120°=60°,
∴OB=OC,∠ABC=90°-∠BAD=30°,
∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DCO=∠DBO,
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°;
故①正确;
∵∠APC+∠DCP+∠PBC=180°,
∴∠APC+∠DCP=150°,
∵∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°,
∴∠POC=180°-(∠OPC+∠OCP)=60°,
∵OP=OC,
∴△OPC是等边三角形;
故②正确;
在AC上截取AE=PA,
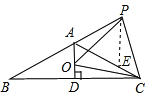
∵∠PAE=180°-∠BAC=60°,
∴△APE是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,
∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,
∴∠APO=∠CPE,
∵OP=CP,
在△OPA和△CPE中,
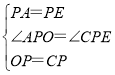
∴△OPA≌△CPE(SAS),
∴AO=CE,
∴AC=AE+CE=AO+AP;
故③正确;
过点C作CH⊥AB于H,
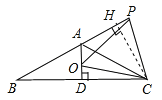
∵∠PAC=∠DAC=60°,AD⊥BC,
∴CH=CD,
∴S△ABC=![]() AB
AB![]() CH,
CH,
S四边形AOCP=S△ACP+S△AOC=![]() AP
AP![]() CH+
CH+![]() OA
OA![]() CD=
CD=![]() AP
AP![]() CH+
CH+![]() OA
OA![]() CH=
CH=![]() CH
CH![]() (AP+OA)=
(AP+OA)=![]() CH
CH ![]() AC,
AC,
∴S△ABC=S四边形AOCP;
故④正确.
故选D.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接“五一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:已知:用3600元购进甲种运动鞋的数量与用3000元购进乙种运动鞋的数量相同.

(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21600元,且不超过22440元,问该专卖店有多少种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.
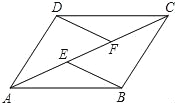
求证:(1)△AFD≌△CEB;(2)四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( )
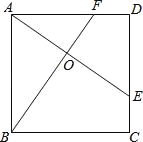
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com