练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，E，F是四边形ABCD对角线AC上的两点，AD∥BC，DF∥BE，AE=CF．

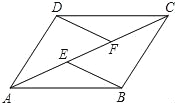
    求证：（1）△AFD≌△CEB；（2）四边形ABCD是平行四边形．

    【答案】（1）证明见解析；（2）证明见解析.

    【解析】

    试题分析：（1）根据全等三角形的判定定理ASA证得△AFD≌△CEB；

    （2）利用（1）中的全等三角形的对应边相等得到AD=CB，则由“有一组对边相等且平行的四边形是平行四边形”证得结论．

    试题解析：（1）如图，∵AD∥BC，DF∥BE，

    ∴∠1=∠2，∠3=∠4．

    又AE=CF，

    ∴AE+EF=CF+EF，即AF=CE．

    在△AFD与△CEB中，

    ，

    ∴△AFD≌△CEB（ASA）；

    （2）由（1）知，△AFD≌△CEB，则AD=CB．

    又∵AD∥BC，

    ∴四边形ABCD是平行四边形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线y=-x+b分别与x轴、y轴交于点A、B，且点A的坐标为（4，0），四边形ABCD是正方形．

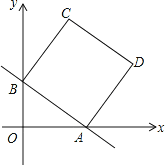
    （1）填空：b= ；

    （2）求点D的坐标；

    （3）点M是线段AB上的一个动点（点A、B除外），试探索在x上方是否存在另一个点N，使得以O、B、M、N为顶点的四边形是菱形？若不存在，请说明理由；若存在，请求出点N的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰三角形ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，下面的结论:①∠APO+∠DCO=30°；②△OPC是等边三角形；③AC=AO+AP；④．其中所有正确结论的序号为 ( )

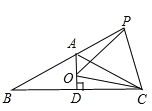
    A.①②③ B．①②④ C．①③④ D．①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正三角形、正方形、等腰直角三角形、平行四边形中，既是轴对称图形又是中心对称图形的是（ ）
    A.正三角形
    B.正方形
    C.等腰直角三角形
    D.平行四边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：－7－2＝____________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一次课堂练习，小璇同学做了如下4道因式分解题，你认为小璇做得不正确的一题是(　　)

    A. a3－a＝a(a2－1)

    B. m2－2mn＋n2＝(m－n)2

    C. x2y－xy2＝xy(x－y)

    D. x2－y2＝(x－y)(x＋y)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将纸片△ABC沿DE折叠使点A落在A′处的位置．

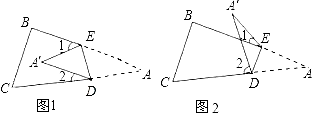
    （1）如果A′落在四边形BCDE的内部（如图1），∠A′与∠1+∠2之间存在怎样的数量关系？并说明理由．

    （2）如果A′落在四边形BCDE的BE边上，这时图1中的∠1变为0°角，则∠A′与∠2之间的关系是 ．

    （3）如果A′落在四边形BCDE的外部（如图2），这时∠A′与∠1、∠2之间又存在怎样的数量关系？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的周长为40米，甲、乙两人分别从A、B同时出发，沿正方形的边行走，甲按逆时针方向每分钟行55米，乙按顺时针方向每分钟行30米．

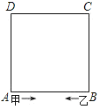
    （1）出发后 分钟时，甲乙两人第一次在正方形的顶点处相遇；

    （2）如果用记号（a，b）表示两人行了a分钟，并相遇过b次，那么当两人出发后第一次处在正方形的两个相对顶点位置时，对应的记号应是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知当x=1时，2ax2+bx的值为3，则当x=2时，ax2+bx的值为 ．

    查看答案和解析>>

    同步练习册答案