
【题目】如图,在平面直角坐标系中,直线y=-![]() x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形.
x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形.
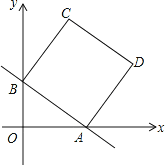
(1)填空:b= ;
(2)求点D的坐标;
(3)点M是线段AB上的一个动点(点A、B除外),试探索在x上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标.
【答案】(1)3;(2) 点N的坐标为(-2,![]() )、(
)、(![]() ,
,![]() )..
)..
【解析】
试题分析:(1)把(4,0)代入y=-![]() x+b即可求得b的值;
x+b即可求得b的值;
(2)过点D作DE⊥x轴于点E,证明△OAB≌△EDA,即可求得AE和DE的长,则D的坐标即可求得;
(3)分当OM=MB=BN=NO时;当OB=BN=NM=MO=3时两种情况进行讨论.
试题解析:(1)把(4,0)代入y=-![]() x+b,得:-3+b=0,解得:b=3,
x+b,得:-3+b=0,解得:b=3,
(2)如图1,过点D作DE⊥x轴于点E,
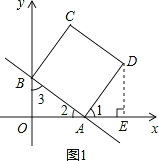
∵正方形ABCD中,∠BAD=90°,
∴∠1+∠2=90°,
又∵直角△OAB中,∠1+∠2=90°,
∴∠1=∠3,
在△OAB和△EDA中,
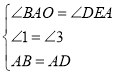 ,
,
∴△OAB≌△EDA,
∴AE=OB=3,DE=OA=4,
∴OE=4+3=7,
∴点D的坐标为(7,4);
(3)存在.
①如图2,当OM=MB=BN=NO时,四边形OMBN为菱形.
则MN在OB的中垂线上,则M的纵坐标是![]() ,
,
把y=![]() 代入y=-
代入y=-![]() x+4中,得x=2,即M的坐标是(2,
x+4中,得x=2,即M的坐标是(2,![]() ),
),
则点N的坐标为(-2,![]() ).
).

②如图3,当OB=BN=NM=MO=3时,四边形BOMN为菱形.
∵ON⊥BM,
∴ON的解析式是y=![]() x.
x.
根据题意得:
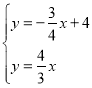 ,解得:
,解得: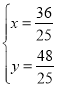 .
.
则点N的坐标为(![]() ,
,![]() ).
).


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,正确的有( )
①无限小数都是有理数;②不循环小数不是有理数;
③不是有理数的数都是无限小数;④0是有理数
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )

A.130° B.150° C.160° D.170°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.
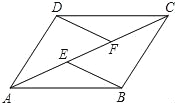
求证:(1)△AFD≌△CEB;(2)四边形ABCD是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com