
 如图,等腰三角形ABC中,∠AC=90°,D,E分别为AB,AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD,交BE于点G,交AC于点M.
如图,等腰三角形ABC中,∠AC=90°,D,E分别为AB,AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD,交BE于点G,交AC于点M.分析 (1)先判定△ACD≌△ABE(SAS),得出∠ADC=∠AEB,再根据同角的余角相等,得出∠CMG=∠ADC,进而得到∠CMG=∠AEB,最后根据等角对等边得出结论;
(2)先过B作AB的垂线,交MF的延长线于N,根据ASA判定△ABF≌△NBF,得出对应边相等,对应角相等,再根据同角的余角相等,得出∠GBN=∠BAF=∠N,进而判定BG=NG,最后根据线段的和差关系得出结论.
解答 证明:(1)∵等腰直角三角形ABC中,∠BAC=90°,
∴AC=AB,∠ACB=∠ABC=45°,
又∵AD=AE,∠CAD=∠BAE,
∴△ACD≌△ABE(SAS),
∴∠ADC=∠AEB,
又∵∠CAD=90°,MF⊥CG,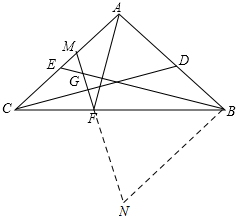
∴∠ADC+∠ACD=90°,∠CMG+∠ACD=90°,
∴∠CMG=∠ADC,
∴∠CMG=∠AEB,
∴EG=MG;
(2)如图,过B作AB的垂线,交MF的延长线于N,则∠NBF=∠ABC=45°,
由(1)可得,△ACD≌△ABE,
∴∠ACD=∠ABE,
又∵∠ACB=∠ABC=45°,
∴∠GCF=∠EBF,
又∵FM⊥CD,AF⊥BE,
∴∠GFC=∠AFB,而∠GFC=∠NFB,
∴∠AFB=∠NFB,
由∠NBF=∠ABF,BF=BF,∠AFB=∠NFB,可得△ABF≌△NBF(ASA),
∴AF=NF,∠N=∠FAB,
∵AB⊥NB,AF⊥BE,
∴∠GBN+∠ABE=90°,∠BAF+∠ABE=90°,
∴∠GBN=∠BAF=∠N,
∴GN=GB,
即GF+FN=GB,
∴GF+AF=GB.
点评 本题考查了全等三角形的判定及性质的运用,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.解决第二问的证明时,要学会判断三条线段之间的关系,一般都需要转化到同一条直线上进行.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
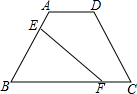 如图,E是等腰梯形ABCD的腰AB上一动点,F是BC上一动点,AB=CD=4,AD=3,BC=9,EF平分梯形的周长,那么BF的最小值为( )
如图,E是等腰梯形ABCD的腰AB上一动点,F是BC上一动点,AB=CD=4,AD=3,BC=9,EF平分梯形的周长,那么BF的最小值为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
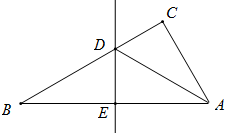 如图,Rt△ABC中,∠C=90°,AB边上的中垂线分别交BC、AB于点D、E,若AE=AC=4cm,△ADC的周长为4$\sqrt{3}$+4cm.
如图,Rt△ABC中,∠C=90°,AB边上的中垂线分别交BC、AB于点D、E,若AE=AC=4cm,△ADC的周长为4$\sqrt{3}$+4cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
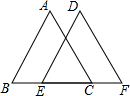 △ABC和△FED中,BE=FC,∠A=∠D.当添加条件∠B=∠DEC时(只需填写一个你认为正确的条件),就可得到△ABC≌△DFE,依据是AAS.
△ABC和△FED中,BE=FC,∠A=∠D.当添加条件∠B=∠DEC时(只需填写一个你认为正确的条件),就可得到△ABC≌△DFE,依据是AAS.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图1,一长方体的长、宽、高分别如图所示.(注:①、②两小题中每个小正方形的边长均为1个单位)
(1)如图1,一长方体的长、宽、高分别如图所示.(注:①、②两小题中每个小正方形的边长均为1个单位)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com