
| A. | k=0 | B. | k≥-1且k≠0 | C. | k≥-1 | D. | k>-1 |
分析 讨论:当k=0时,方程化为-3x-$\frac{9}{4}$=0,方程有一个实数解;当k≠0时,△=(-3)2-4k•(-$\frac{9}{4}$)≥0,然后求出两个中情况下的k的公共部分即可.
解答 解:当k=0时,方程化为-3x-$\frac{9}{4}$=0,解得x=$\frac{3}{4}$;
当k≠0时,△=(-3)2-4k•(-$\frac{9}{4}$)≥0,解得k≥-1,
所以k的范围为k≥-1.
故选C.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.


科目:初中数学 来源: 题型:填空题
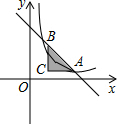 如图,过C(2,1)作AC∥x轴,BC∥y轴,点A,B都在直线y=-x+6上,若双曲线y=$\frac{k}{x}$(x>0)与△ABC总有公共点,则k的取值范围是2≤k≤9.
如图,过C(2,1)作AC∥x轴,BC∥y轴,点A,B都在直线y=-x+6上,若双曲线y=$\frac{k}{x}$(x>0)与△ABC总有公共点,则k的取值范围是2≤k≤9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
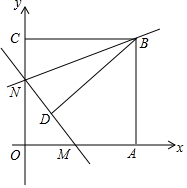 如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足方程|x-15|+$\sqrt{y-13}$=0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=$\frac{3}{4}$
如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足方程|x-15|+$\sqrt{y-13}$=0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=$\frac{3}{4}$查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
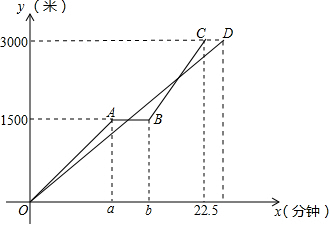 “低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 28°,30° | B. | 30°,28° | C. | 31°,30° | D. | 30°,30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com