
分析 根据已知条件得到:p2-3p=4q2-6q=2,利用因式分解法分别求得p、q的值,然后代入所求的代数式进行求值即可.
解答 解:∵由p2=3p+2得:p2-3p=2.
由2q2=3q+1得:4q2=6q+2,
∴4q2-6q=2,
则p2-3p=4q2-6q,
∴p2-3p-4q2+6q=(p+2q)(p-2q)-3(p-2q)=(p-2q)(p+2q-3)=0,
∵p≠2q,
∴p+2q-3=0,
∴p+2q=3,
∴p2+4q2=(2+3p)+(6q+2)=3(p+2q)+4=9+4=13.即p2+4q2=13.
点评 本题考查了因式分解的应用.解题时,注意“整体代入”数学思想的应用.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:选择题
| A. | 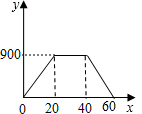 | B. | 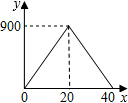 | ||
| C. | 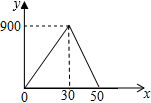 | D. | 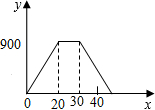 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC绕A逆时针旋转使得C点落在BC 边上的F 处,则对于结论①AC=AF;②∠FAB=∠EAB; ③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是( )
如图,△ABC绕A逆时针旋转使得C点落在BC 边上的F 处,则对于结论①AC=AF;②∠FAB=∠EAB; ③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
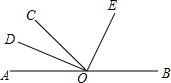 ∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.
∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.| A. | 60° | B. | 65° | C. | 90° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
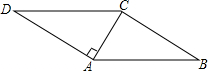 在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是( )
在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是( )| A. | 4+2$\sqrt{3}$ | B. | 8 | C. | 8+4$\sqrt{3}$ | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com