
已知:关于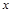 的二次函数y=px2-(3p+2)x+2p+2(p>0)
的二次函数y=px2-(3p+2)x+2p+2(p>0)
(1)求证:无论p为何值时,此函数图象与x轴总有两个交点;
(2)设这两个交点坐标分别为(x1,0),(x2,0)(其中x1<x2)且S=x2-2x1,求S关于P的函数解析式
科目:初中数学 来源: 题型:
| ||
| 3 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
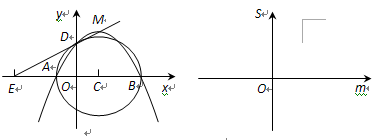
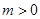 ,点
,点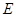 的坐标为
的坐标为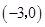 ,关于
,关于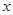 的二次函数
的二次函数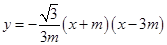 图象的顶点为
图象的顶点为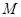 ,图象交
,图象交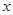 轴于
轴于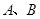 两点,交
两点,交 轴正半轴于
轴正半轴于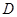 点.以
点.以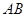 为直径作圆,其圆心为
为直径作圆,其圆心为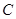 .
. 
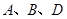 三点的坐标(可用含
三点的坐标(可用含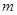 的代数式表示);
的代数式表示); 为何值时
为何值时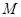 点在直线
点在直线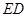 上?判定此时直线
上?判定此时直线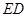 与圆的位置关系?
与圆的位置关系?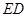 ,当
,当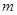 变化时,试用
变化时,试用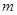 表示
表示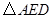 的面积
的面积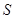 ,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
,并在给出的直角坐标系中画出S关于m的函数图象的示意图.查看答案和解析>>
科目:初中数学 来源:2011-2012学年甘肃省庄浪县阳川中学九年级第一学期期末测试数学卷 题型:解答题
(本题满分9分)已知关于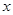 的一元二次方程
的一元二次方程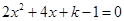 有实数根,
有实数根,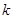 为正整数.
为正整数.
【小题1】(1)求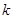 的值;
的值;
【小题2】(2)当此方程有两个非零的整数根时,将关于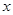 的二次函数
的二次函数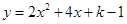 的图象向
的图象向
下平移8个单位,写出平移后的图象的解析式;
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(吉林长春卷)数学(带解析) 题型:解答题
已知两个关于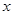 的二次函数
的二次函数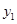 与
与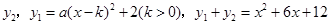 ,当
,当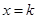 时,
时,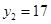 ;且二次函数
;且二次函数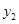 的图象的对称轴是直线
的图象的对称轴是直线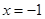 .
.
(1)求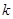 的值;
的值;
(2)求函数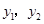 的表达式;
的表达式;
(3)在同一直角坐标系内,问函数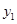 的图象与
的图象与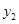 的图象是否有交点?请说明理由.
的图象是否有交点?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com