解:(1)由题意知,抛物线的对称轴为:x=-1,
已知A(-3,0),
故B(1,0).
(2)①∵点B(1,0),C(0,3)在抛物线上,抛物线与y轴交于点C(0,3);
∴

,
解得
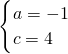
,
∴抛物线所对应的函数关系式为y=-(x+1)
2+4;
∴M(-1,4)设直线MC所对应的函数关系式为y=kx+b,
∴
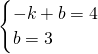
,
解得
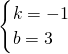
,
∴直线MC所对应的函数关系式为y=-x+3;
②假设在抛物线上存在异于点C的点P,使得△NPC是以NC为直角边的直角三角形.
1)若PN为△NPC的另一条直角边,如图1;

易得直线MC与x轴的交点坐标为N(3,0),
∵OC=ON,
∴∠CNO=45°,
在y轴上取点D(0,-3),连接ND交抛物线于点P,
∵ON=OD,
∴∠DNO=45°,
∴∠PNC=90°.
设直线ND的函数表达式为y=mx+n;
可得

,
解得
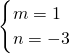
∴直线ND的函数表达式为y=x-3;
设点P(x,x-3),并将它代入抛物线的函数表达式,得x-3=-(x+1)
2+4,
即x
2+3x-6=0,
解得

,

,
∴

,

;
∴满足条件的点为

,
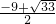
),

,
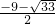
).
2)若PC是另一条直角边,如图2;

∵点A是抛物线与x轴的另一交点,
∴点A的坐标为(-3,0);
连接AC;
∵OA=OC,
∴∠OCA=45°,
又∵∠OCN=45°,
∴∠ACN=90°,
∴点A就是所求的点P
3(-3,0);
第二种解法:求出直线AC的函数表达式为y=x+3;
设点P(x,x+3),代入抛物线的函数表达式,
得x+3=-(x+1)
2+4,
即x
2+3x=0;
解得x
1=-3,x
2=0;
∴y
1=0,y
2=3,
∴点P
3(-3,0),P
4(0,3)(舍去).]
综上可知,在抛物线上存在满足条件的点有3个,分别

,
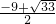
),

,
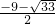
),P
3(-3,0).
分析:(1)根据已知抛物线的解析式,可得到抛物线的对称轴方程,从而根据A点坐标求出点B的坐标.
(2)根据A、B、C三点坐标,即可求得抛物线的解析式和它的顶点坐标;
①已经求得M、C的坐标,利用待定系数法求解即可;
②假设存在符合条件的P点,分两种情况考虑:
1)以N为直角顶点,即PN为另一条直角边;
易求得点N的坐标,根据C、N点的坐标可知∠CNO=45°,若∠PNC=90°,可在y轴截取OD=ON,易得点D的坐标,即可求出直线DN的解析式,联立抛物线的解析式即可得到点P的坐标;
2)以C为直角顶点,即PC为另一条直角边;
根据A、C的纵坐标知:∠CAN=45°,此时∠ACN=90°,那么点A即为所求的P点;
综合上述两种情况,即可得到符合条件的P点坐标.
点评:此题是二次函数的综合题,涉及到二次函数的对称性、用待定系数法确定函数解析式的方法、直角三角形的判定、函数图象交点坐标的求法等知识,需注意的是(2)②中,C、N都有可能是直角顶点,需要分类讨论,以免漏解.

 已知抛物线y=a(x+1)2+c与x轴交于点A(-3,0),
已知抛物线y=a(x+1)2+c与x轴交于点A(-3,0), ,
,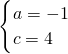 ,
,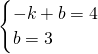 ,
,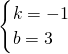 ,
,
 ,
,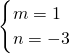
 ,
, ,
, ,
, ;
; ,
,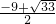 ),
), ,
,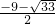 ).
).
 ,
,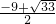 ),
), ,
,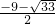 ),P3(-3,0).
),P3(-3,0).

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案 正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为
正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为 廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-
廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-