
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
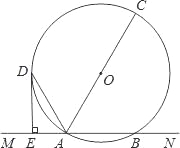
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
【答案】解:(1)证明:连接OD,
∵OA=OD,∴∠OAD=∠ODA。
∵∠OAD=∠DAE,∴∠ODA=∠DAE。∴DO∥MN。
∵DE⊥MN,∴∠ODE=∠DEM =90°,即OD⊥DE。
∵D在⊙O上,∴DE是⊙O的切线。
(2)连接CD,
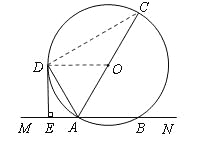
∵∠AED=90°,DE=6,AE=3,∴AD=![]() 。
。
∵AC是⊙O的直径,∴∠ADC=∠AED =90°。
∵∠CAD=∠DAE,∴△ACD∽△ADE。 ∴![]() ,即
,即![]() 。
。
解得:AC=15。
∴⊙O的半径是7.5cm。
【解析】试题分析:(1)连接OD,根据平行线的判断方法与性质可得∠ODE=∠DEM=90°,且D在⊙O上,故DE是⊙O的切线.
(2)由直角三角形的特殊性质,可得AD的长,又有△ACD∽△ADE.根据相似三角形的性质列出比例式,代入数据即可求得圆的半径.
试题解析:(1)证明:连接OD.
∵OA=OD,
∴∠OAD=∠ODA.
∵∠OAD=∠DAE,
∴∠ODA=∠DAE.
∴DO∥MN.
∵DE⊥MN,
∴∠ODE=∠DEM=90°.
即OD⊥DE.
∵D在⊙O上,OD为⊙O的半径,
∴DE是⊙O的切线.
(2)解:∵∠AED=90°,DE=6,AE=3,
∴![]() .
.
连接CD.
∵AC是⊙O的直径,
∴∠ADC=∠AED=90°.
∵∠CAD=∠DAE,
∴△ACD∽△ADE.
∴![]() .
.
∴![]() .
.
则AC=15(cm).
∴⊙O的半径是7.5cm.


科目:初中数学 来源: 题型:
【题目】通过学习同学们已经体会到灵活运用整式乘法公式给计算和化简带来的方便、快捷.相信通过下面材料的学习、探究,会使你大开眼界,并获得成功的喜悦.
例:用简便方法计算195×205.
解:195×205
=(200-5)(200+5) ①
=2002-52 ②
=39975.
(1)例题求解过程中,第②步变形是利用____________(填乘法公式的名称);
(2)用简便方法计算:
①9×11×101×10 001;
②(2+1)(22+1)(24+1)…(232+1)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.

(1)求证:∠F+∠FEC=2∠A;
(2)过B点作BM∥AC交FD于点M,试探究∠MBC与∠F+∠FEC的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春季流感爆发,某校为了解全体学生患流感情况,随机抽取部分班级对患流感人数的进行调查,发现被抽查各班级患流感人数只有1名、2名、3名、4名、5名、6名这六种情况,并制成如下两幅不完整的统计图:
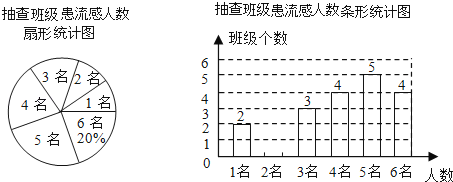
(1)抽查了 个班级,并将该条形统计图(图2)补充完整;
(2)扇形图(图1)中患流感人数为4名所在扇形的圆心角的度数为 ;
(3)若该校有45个班级,请估计该校此次患流感的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省先后出台了居民用电“阶梯价格”制度,如下表是某省的电价标准(每月).例如:方女士家5月份用电500度,电费=180×0.6+220×二档电价+100×三档电价=352元;李先生家5月份用电460度,交费316元.请问表中二档电价、三档电价各是多少?
阶梯 | 电量 | 电价 |
一档 | 0~180度 | 0.6元/度 |
二档 | 181~400度 | 二档电价 |
三档 | 401度及以上 | 三档电价 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC. 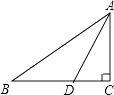
(1)当∠B=40°时,求∠ADC的度数;
(2)若AB=10cm,CD=4cm,求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证: 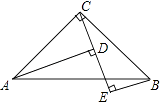
(1)△BEC≌△CDA;
(2)DE=AD﹣BE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com