
【题目】已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.

(1)求证:∠F+∠FEC=2∠A;
(2)过B点作BM∥AC交FD于点M,试探究∠MBC与∠F+∠FEC的数量关系,并证明你的结论.
【答案】(1)证明见解析(2)∠MBC=∠F+∠FEC,证明见解析
【解析】试题分析:(1)根据三角形外角的性质,可得出∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,再根据∠A=∠ABC,即可得出答案;
(2)由BM∥AC,得出∠MBA=∠A,∠A=∠ABC,得出∠MBC=∠MBA+∠ABC=2∠A,结合(1)的结论证得答案即可.
(1)证明:∵∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,
∴∠F+∠FEC=∠F+∠A+∠ADE,
∵∠ADE=∠BDF,
∴∠F+∠FEC=∠A+∠ABC,
∵∠A=∠ABC,
∴∠F+∠FEC=∠A+∠ABC=2∠A.
(2)∠MBC=∠F+∠FEC.
证明:∵BM∥AC,
∴∠MBA=∠A,、
∵∠A=∠ABC,
∴∠MBC=∠MBA+∠ABC=2∠A,
又∵∠F+∠FEC=2∠A,
∴∠MBC=∠F+∠FEC.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在比例尺是1:4000的成都市城区地图上,位于锦江区的九眼桥的长度约为3cm,它的实际长度用科学记数法表示为( )
A.12×103cmB.1.2×102mC.1.2×104mD.0.12×105cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式计算正确的是( )
A. ﹣2a+5b=3abB. 6a+a=6a2
C. 3ab2﹣5b2a=﹣2ab2D. 4m2n﹣2mn2=2mn
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图

(1)请写出在直角坐标系中的房子的A、B、C、D、E、F、G的坐标。
(2)源源想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的7个点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
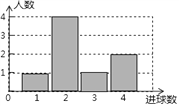
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
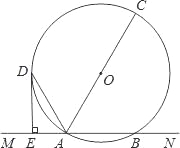
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com