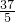
或7
分析:等腰三角形ABC中a可能是底边,也可能是腰,应分两种情况进行讨论.①当a是腰时,则方程有一个根是3,代入即可求得m的值,从而求解;②当a是底边时,方程有两个相等的实根,根据一元二次方程根的情况与判别式△的关系,从而求得其周长.
解答:∵b、c是关于x的方程x
2+mx+2-

m=0的两个实数根,
∴b+c=-m,bc=2-

m.
分两种情况:
①当a为其腰时,则b=a,或c=a,
∴方程必有一个根为3,
代入方程得:9+3m+2-

m=0,
解得m=-

,
则b+c=

,
则周长是a+b+c=
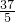
;
②当a为其底时,b=c,原方程有两个相等的实数根,
∴△=m
2-4×(2-

m)=0,
∴m
1=-4,m
2=2>0(舍去),
∵b+c=4>a,bc=4>0,
∴m=-4符合题意,
∴a+b+c=3+4=7.
∴△ABC的周长为
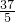
或7.
故答案为:
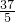
或7.
点评:本题考查了一元二次方程根的情况与判别式△的关系,一元二次方程根与系数的关系,等腰三角形的性质及三角形的三边关系定理.难度中等.根据等腰三角形的性质,将a边进行分类是解题的关键.
一元二次方程ax
2+bx+c=0(a≠0)的根与△=b
2-4ac有如下关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根;
一元二次方程根与系数的关系:如果x
1,x
2是一元二次方程ax
2+bx+c=0(a≠0)的两根,那么x
1+x
2=-

,x
1x
2=

,反过来也成立,即

=-(x
1+x
2),

=x
1x
2.
三角形的三边关系定理:两边之和大于第三边,两边之差小于第三边.

 m=0的两个根,则三角形ABC的周长等于________.
m=0的两个根,则三角形ABC的周长等于________.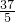 或7
或7 m=0的两个实数根,
m=0的两个实数根, m.
m. m=0,
m=0, ,
, ,
,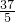 ;
; m)=0,
m)=0,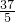 或7.
或7.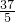 或7.
或7. ,x1x2=
,x1x2= ,反过来也成立,即
,反过来也成立,即 =-(x1+x2),
=-(x1+x2), =x1x2.
=x1x2.

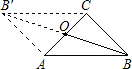 在等腰三角形ABC中,∠C=90°,BC=2cm.如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,那么点B′与点B的原来位置相距
在等腰三角形ABC中,∠C=90°,BC=2cm.如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,那么点B′与点B的原来位置相距