
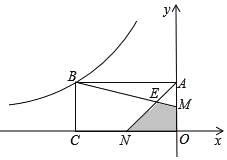
【题目】如图,矩形OABC的两边OA、OC在坐标轴上,且OC=2OA,M、N分别为OA、OC的中点,BM与AN交于点E,若四边形EMON的面积为2,则经过点B的双曲线的解析式为( )
A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=﹣
D. y=﹣![]()
【答案】A
【解析】过M作MG∥ON,交AN于G,过E作EF⊥AB于F,如图所示:
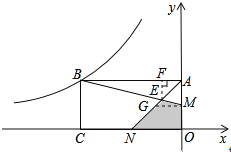
设EF=h,OM=a,
那么由题意可知:AM=OM=a,ON=NC=2a,AB=OC=4a,BC=AO=2a
△AON中,MG∥ON,AM=OM,
∴MG=![]() ON=a,
ON=a,
∵MG∥AB
∴![]() =
=![]() =
=![]() ,
,
∴BE=4EM,
∵EF⊥AB,
∴EF∥AM,
∴![]() =
=![]() =
=![]() .
.
∴FE=![]() AM,即h=
AM,即h=![]() a,
a,
∵S△ABM=4a×a÷2=2a2,
S△AON=2a×2a÷2=2a2,
∴S△ABM=S△AON,
∴S△AEB=S四边形EMON=2,
S△AEB=AB×EF÷2=4a×h÷2=2,
ah=1,又有h=![]() a,a=
a,a=![]() (长度为正数)
(长度为正数)
∴OA=![]() ,OC=2
,OC=2![]() ,因此B的坐标为(-2
,因此B的坐标为(-2![]() ,
,![]() ),
),
那么经过B的双曲线的解析式就是y=-![]() ;
;
故选A。


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若sinB=![]() ,EF=2
,EF=2![]() ,求CD的长.
,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )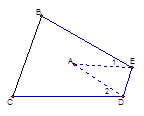
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2012四川雅安)在平面直角坐标系中,三角形ABC的三个顶点坐标分别是A(4,5),B(1,2),C(4,2),将三角形ABC向左平移5个单位后,A点的对应点A′的坐标是( )
A.(0,5)
B.(-1,5)
C.(9,5)
D.(-1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展捐书活动,以下是5名同学捐书的册数:4,9,5,x,3,已知这组数据的平均数是5,则这组数据的中位数和众数分别是( )
A. 3和3 B. 4和4 C. 3和4 D. 5和5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程2x2﹣5x﹣4=0根的情况是( )
A. 有两个不相等的实数根
B. 有两个相等的实数根
C. 没有实数根
D. 无法判定该方程根的情况
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com