
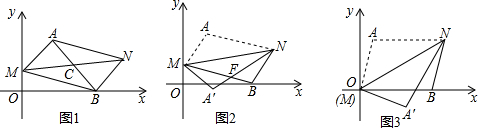
���� ��1������AASֱ���жϳ���ACN�ա�BCM���ɣ�
��2�����۵������ʵó���ANM=��A'NM�����ɵó����ۣ�
��3����ȷ������N�����꣬����ȷ����OE������FM=FN������ù��ɶ������OF�����ɵó���F�����꣬�����ô���ϵ�����ó����ۣ�
��� �⣺��1����AN��MB�����BAN=��ABM����ANM=��BMN��
�ߵ�C��AB���е㣬��AC=BC��
�ڡ�ACN�͡�BCM�У�$\left\{\begin{array}{l}{��ANM=��BMN}\\{��BAN=��ABM}\\{AC=BC}\end{array}\right.$��
���ACN�ա�BCM��AAS����
��AN=BM��
��AN��BM��
���ı���AMBN��ƽ���ı��Σ�
��2���ɣ�1��֪����ANM=��BMN��
�߽���AMN��ֱ��MN���ۣ��á�MA��N��A��N��MB�ڵ�F��
���ANM=��A'NM��
���BMN=A'NM��
��FM=FN��
��3����ͼ�� ����M�ƶ���������
����M�ƶ���������
ԭ��O�غ�ʱ��BM=OB
��A��2��4����B��6��0����
��OA=2$\sqrt{5}$��OB=6=BM��
�ɣ�1��֪���ı���AMBN��ƽ���ı��Σ�
��AN��OB��AN=BM=6��
��N��8��4����
����AMN��ֱ��MN���ۣ��á�MA��Nʱ����A��N��MB�ڵ�F��
�ɣ�2��֪��FM=FN��
����N��NE��BM��
��E��8��0����NE=4��
���F��m��0������OF=m��
��FN=m��
��EF=8-m��
��Rt��EFN��EF2+EN2=FN2��
�ࣨ8-m��2+16=m2��
��m=5��
��F��5��0����
��ֱ��A'N�Ľ���ʽΪy=kx+b��
��N��8��4����
��$\left\{\begin{array}{l}{5k+b=0}\\{8k+b=4}\end{array}\right.$��
��$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-\frac{20}{3}}\end{array}\right.$��
��ֱ��AN'�Ľ���ʽΪy=$\frac{4}{3}$x-$\frac{20}{3}$��
���� ������һ�κ����ۺ��⣬��Ҫ������ȫ�������ε��ж������ʣ��۵������ʣ����������ε��ж������ɶ���������ϵ�������Ȿ��ùؼ��ǵó�FM=FN����һ���е��ѵ���п������⣮


 С�����ϵ�д�
С�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʹ��Բ���ֱ�߷ֱ���AOB�͡�BOC�Ľ�ƽ����OM��ON�������MON=68�㣬��ô��
��ͼ��ʹ��Բ���ֱ�߷ֱ���AOB�͡�BOC�Ľ�ƽ����OM��ON�������MON=68�㣬��ô���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2-y2 | B�� | -x2+y2 | C�� | 4x2y2-1 | D�� | -x2-y2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
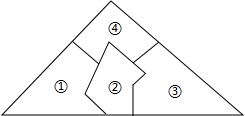 һ�������β�����С��������Ŀ飨��ͼ����Ϊ����һ�����ǰһ���IJ�����С��ֻ������е�����ȥ�����꼴�ɣ���������ѡ����ǣ�������
һ�������β�����С��������Ŀ飨��ͼ����Ϊ����һ�����ǰһ���IJ�����С��ֻ������е�����ȥ�����꼴�ɣ���������ѡ����ǣ�������| A�� | �����е��������� | B�� | ���ٺ͢� | ||
| C�� | ���ٺ͢� | D�� | ���ۺ͢� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
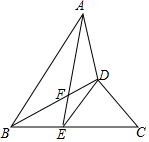 ��ͼ���߶�BDƽ�֡�ABC����AB=BC��E���߶�BC��һ�㣬DE=DC������AE��BD�ڵ�F��
��ͼ���߶�BDƽ�֡�ABC����AB=BC��E���߶�BC��һ�㣬DE=DC������AE��BD�ڵ�F���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com