
 如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE.连接BG并延长与AC交于点F,若AD=9,CE=12,则GF为5.
如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE.连接BG并延长与AC交于点F,若AD=9,CE=12,则GF为5. 分析 根据重心的性质得到AG=$\frac{2}{3}$AD=6,CG=$\frac{2}{3}$CE=8,根据勾股定理求出AC,根据直角三角形的性质计算即可.
解答 解:∵点G是△ABC的两条中线AD、CE的交点,
∴点G是△ABC的重心,
∴AG=$\frac{2}{3}$AD=6,CG=$\frac{2}{3}$CE=8,
∵AD⊥CE,
∴AC=$\sqrt{A{G}^{2}+C{G}^{2}}$=10,
∵点G是△ABC的重心,
∴点F是AC的中点,
∴GF=$\frac{1}{2}$AC=5,
故答案为:5.
点评 本题考查的是三角形的重心的概念和性质:三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
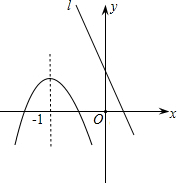 已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=-1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<-1<x1<x2,则y1,y2,y3的大小关系是( )
已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=-1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<-1<x1<x2,则y1,y2,y3的大小关系是( )| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,AB=15,AC=9,则tan∠ADC=( )
如图,AB是⊙O的直径,AB=15,AC=9,则tan∠ADC=( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{2}{3}}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{2}{9}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 平均分 | 甲班 | 乙班 |
| 男生 | 86 | 95 |
| 女生 | 94 | 88 |
| 全班 | 89 | 92 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com