
����Ŀ���ڽ���Σ����Ӱ���£����Ҳ�ȡ������������ߣ�����Ͷ�ʳ�Ϊ����������ǿ����������.�ֽ�ǿ��˾�б�һ��̣��ڼס�������ʩ�������м���������30̨���ҵ���������26̨����˾��A��B���طֱ���������32̨��24̨���ִ�A����һ̨���ס������صķ��÷ֱ���400Ԫ��300Ԫ����B����һ̨���ס������صķ��÷ֱ�Ϊ200Ԫ��500Ԫ.�����A��������![]() ̨���������˼ס�������������������������ܷ���Ϊ
̨���������˼ס�������������������������ܷ���Ϊ![]() Ԫ.
Ԫ.
��1����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2����˾Ӧ��������ķ�������ʹ�����������������ܷ������٣�
���𰸡���1��![]() =400x+12600
=400x+12600
(2) ��B��������30��6=24��̨���������ҵ�26����32��6��=0��̨�� ������
�����������������
(1) ����������з������ɽ����غ�ʩ����֮�������������������б�������
�� | �ҵ� | �ϼ� | |
A�� | x (̨) | 32-x (̨) | A�ؿ�棺32 (̨) |
B�� | 30-x (̨) | 26-(32-x)=24-(30-x)=x-6 (̨) | B�ؿ�棺24 (̨) |
�ϼ� | ������30 (̨) | �ҵ�����26 (̨) | �ܼ���56 (̨) |
�����ϱ��еĸ���֮������������Լ���Ŀ�����������䵥�ۣ����������������ܼ�=���䵥�ۡ������������г�������ã����֮�����������ܷ��õı���ʽ.
(2) ������(1)���еõ����ܷ��ñ���ʽ��֪���ܷ���y������x(��A�������ص�������������)�����Ӷ����ӵ�. ��ˣ�ֻҪ�õ�x����Сֵ�Ϳ��Ի���ܷ��õ���Сֵ. ����(1)�е�����������ϵ�����Կ�����x��ȡֵ���뱣֤����֮�������������Ϊ�Ǹ���. �ݴ˿ɵõ�һ������x�IJ���ʽ�飬��֮���ɻ��x��ȡֵ��Χ�������õ��ܷ��õ���Сֵ.
���������
(1) �������������A�������ص�������������Ϊx̨�����A�������ҵص�������������ӦΪ(32-x)̨����B�������ص�������������ӦΪ(30-x)̨����B�������ҵص�������������ӦΪ[26-(32-x)]̨. �����
��A���������������ķ���Ϊ��400x��
��A�����ҵ����������ķ���Ϊ��300(32-x)��
��B���������������ķ���Ϊ��200(30-x)��
��B�����ҵ����������ķ���Ϊ��500[26-(32-x)].
���˼ס�������������������������ܷ���y���Ա�ʾΪ��
y=400x+300(32-x)+200(30-x)+500[26-(32-x)]=400x+12600��
��y=400x+12600.
(2) ���ڸ���֮���������������x��ȡֵ�й�. ��ʵ�����������x��ȡֵ���뱣֤����֮�������������Ϊ�Ǹ���. �����x��ȡֵ�������㣺
 ��
��
��˲���ʽ�飬��
6��x��30.
�������������������ܷ���y�ʹ�A�������ص�������������x�Ĺ�ϵy=400x+12600��֪��y��x����һ�κ�����ϵ����y��x����������. ��Ҫʹ�ܷ���y��С����xӦȡ��Сֵ.
����Ϊx��ȡֵ��ΧΪ��6��x��30�����Ե�x=6ʱ���ܷ�����С.
�ܷ������ٵ����䷽��Ϊ��
��A�������ص�������������Ϊ��6̨��
��A�������ҵص�������������Ϊ��26̨��
��B�������ص�������������Ϊ��24̨��
��B�������ҵص�������������Ϊ��0̨.
����(1) y��x�ĺ�����ϵʽΪ��y=400x+12600.
(2) �ܷ������ٵ����䷽��Ϊ����A��������6̨����������A�����ҵ���26̨����������B��������24̨������������B�����ҵ���������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�
��1�����ó߹�����ABC��ƽ����BE����AD��E��������ͼ�ۼ�����д��������
��2���ڣ�1��������ͼ���У���֤��AB=AE��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���E��F�ڶԽ���AC�ϣ���AE=CF����֤���ı���BEDF��ƽ���ı��Ρ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�ij�˿ͳ˸����г��Ӽؾ����ҵص����أ��г�������ʻ��ͼ��Ϊ�г����ҵ�·��y(ǧ��)����ʻʱ��x(Сʱ)�ĺ�����ϵͼ��
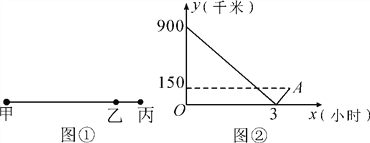
(1)��գ��ס������ؾ���_______ǧ�ף�
(2)������г����ҵص�·��y����ʻʱ��x֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A.��a2��3=a6
B.a2+a2=a4
C.��3a����2a��2=6a
D.3a��a=3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com