
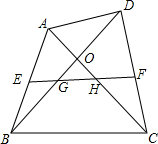
 如图,在四边形ABCD中,AC与BD交于点O,E为AB中点,F为CD中点,EF分别与BD、AC交于点G、H.
如图,在四边形ABCD中,AC与BD交于点O,E为AB中点,F为CD中点,EF分别与BD、AC交于点G、H.分析 (1)取BC的中点,连接ME、MF,根据三角形中位线定理得到EM=$\frac{1}{2}$AC,FM=$\frac{1}{2}$BD,得到ME=MF,得到答案;
(2)证明△OGH∽△MFE,根据相似三角形的性质证明结论.
解答 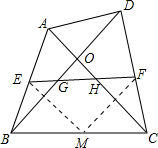 (1)解:OG=OH.
(1)解:OG=OH.
证明如下:
取BC的中点,连接ME、MF,
则EM=$\frac{1}{2}$AC,FM=$\frac{1}{2}$BD,又AC=BD,
∴ME=MF,
∴∠MFE=∠MEF,
∵ME∥AC,MF∥BD,
∴∠MFE=∠OGH,∠OHG=∠MEF,
∴∠OGH=∠OHG,
∴OG=OH;
(2)∵∠MFE=∠OGH,∠OHG=∠MEF,
∴△OGH∽△MFE,
∴$\frac{OG}{MF}$=$\frac{OH}{ME}$,
∴$\frac{OG}{2MF}$=$\frac{OH}{2ME}$,即$\frac{OG}{BD}$=$\frac{OH}{AC}$,
∴OG•AC=OH•BD.
点评 本题考查的是三角形中位线定理和相似三角形的判定和性质,掌握三角形的中位线平行于第三边且等于第三边的一半是解题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
 如图,公里MN和小路PQ在点P处交汇,小路PQ上有一所学校A到公路MN的距离为80m,假如拖拉机行驶时,周围100m内受噪声影响,那么拖拉机在公路MN上沿PN方向行驶时,学校A是否受到噪声影响?如果学校A受到影响,已知拖拉机速度为18km/h,那么学校A受到影响的时间为多长?
如图,公里MN和小路PQ在点P处交汇,小路PQ上有一所学校A到公路MN的距离为80m,假如拖拉机行驶时,周围100m内受噪声影响,那么拖拉机在公路MN上沿PN方向行驶时,学校A是否受到噪声影响?如果学校A受到影响,已知拖拉机速度为18km/h,那么学校A受到影响的时间为多长?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,2) | B. | (3,-2) | C. | (-2,-3) | D. | (2,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
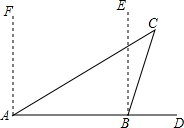 如图,一艘轮船上午8时在A处沿正东方向行驶,在A处测得灯塔C在北偏东60°方向上,行驶1小时后到达B处,在B处测得灯塔C在北偏东20°方向上.求△ABC各内角及∠DBC的度数.
如图,一艘轮船上午8时在A处沿正东方向行驶,在A处测得灯塔C在北偏东60°方向上,行驶1小时后到达B处,在B处测得灯塔C在北偏东20°方向上.求△ABC各内角及∠DBC的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com