Question

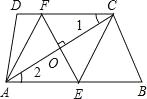
【题目】如图，在梯形ABCD中，AB∥DC，过对角线AC的中点O作EF⊥AC，分别交边AB、CD于点E、F，连接CE、AF．

（1）求证：四边形AECF是菱形；

（2）若EF=4，tan∠OAE=，求四边形AECF的面积．

Answer 1

【答案】（1）证明详见解析；（2）20.

【解析】

试题分析：（1）运用“对角线互相垂直平分的四边形是菱形”判定，已知EF⊥AC，AO=OC，只需要证明OE=OF即可，用全等三角形得出；

（2）菱形的面积可以用对角线积的一半来表示，由已知条件，解直角三角形AOE可求AC、EF的长度．

试题解析：（1）证明：方法1：

∵AB∥DC，

∴∠1=∠2．

在△CFO和△AEO中，∠1=∠2，∠FOC=∠EOA，OC=OA，

∴△CFO≌△AEO，

∴OF=OE，

又∵OA=OC，

∴四边形AECF是平行四边形．

∵EF⊥AC，

∴四边形AECF是菱形．

方法2：证△AEO≌△CFO同方法1，

∴CF=AE，

∵CF∥AE，

∴四边形AFCE是平行四边形．

∵OA=OC，EF⊥AC，

∴EF是AC的垂直平分线，

∴AF=CF，

∴四边形AECF是菱形．

（2）解：∵四边形AECF是菱形，EF=4，

∴OE=EF=×4=2．

在Rt△AEO中，

∵tan∠OAE=，

∴OA=5，

∴AC=2AO=2×5=10．

∴=EFAC=×4×10=20．