
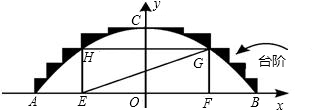
 某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,量得该拱桥占地面最宽处AB=20米,最高处点C距地面5米(即OC=5米)
某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,量得该拱桥占地面最宽处AB=20米,最高处点C距地面5米(即OC=5米) 解:(1)因为OC=5米,所以顶点C(0,5),c=5,
解:(1)因为OC=5米,所以顶点C(0,5),c=5,| 1 |
| 20 |
| 1 |
| 20 |
| 1 |
| 20 |
| 1 |
| 20 |
| 1 |
| 20 |
| 1 |
| 20 |
| 1 |
| 20 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 1 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 20 |

查看答案和解析>>
科目:初中数学 来源: 题型:
某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为且过顶点C(0,5)(长度单位:m)
(1)直接写出c的值;
(2)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5 m的地毯,地毯的价格为20元/ ,求购买地毯需多少元?
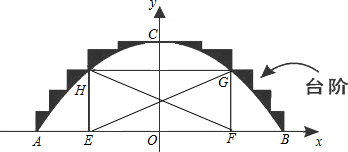
 (3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5 m,求斜面EG的倾斜角∠GEF的正切值.
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5 m,求斜面EG的倾斜角∠GEF的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com