
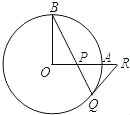
【题目】如图,OA和OB是⊙O的半径,OB=2,OA⊥OB,P是OA上任一点,BP的延长线交⊙O于点Q,过点Q的⊙O的切线交OA延长线于点R.
(1)求证:RP=RQ;
(2)若OP=PQ,求PQ的长.
【答案】(1)证明见解析(2)![]()
【解析】
(1)连接OQ,由QR为圆O的切线,得到∠OQR为90°,即∠OQB+∠PQR=90°,由OA与OB垂直,根据垂直的定义得到∠BOA=90°,所以∠B+∠BPO=90°,再根据对顶角相等及等角的余角相等,得到∠RPQ=∠RQP,根据“等角对等边”得证;
(2)根据OP=PQ,由“等边对等角”得到∠POQ=∠PQO,又根据半径OB=OQ,再根据“等边对等角”得到∠B=∠BQO,在三角形OBQ中,由∠BOA为直角,设出∠B=∠PQO=∠POQ=x,根据三角形的内角和定理列出关于x的方程,求出方程的解得到x的值,即为∠B的度数,又∠RPQ=∠BPO=60°,PR=QR,所以三角形PRQ为等边三角形,所以PQ=QR,在直角三角形OQR中,根据30°的正切函数定义,由OQ=OB=2,即可求出QR的值,从而得到PQ的长.
(1)连接OQ.∵QR是切线,∴∠OQR=90°,∴∠BQO+∠PQR=90°.
∵OA⊥OB,∴∠BOA=90°,∴∠B+∠BPO=90°,又∠BPO=∠RPQ,∴∠B+∠RPQ=90°.
由OB=OQ得:∠B=∠BQO,∴∠RPQ=∠RQP,∴PR=QR;
(2)∵OP=PQ,∴∠POQ=∠PQO,
又OB=OQ,∴∠B=∠PQO,
设∠B=∠PQO=∠POQ=x,又∠BOP=90°,
根据三角形内角和定理得:
∠B+∠BOP+∠POQ+∠PQO=180°,即x+90°+x+x=180°,
解得:x=30°,即∠B=30°,∴∠RPQ=∠BPO=60°,又PR=QR,∴△PQR为等边三角形,即PQ=QR=PR,
在直角三角形OQR中,OQ=OB=2,
根据锐角三角函数定义得:
![]() .
.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】(2016湖南省株洲市)某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,反比例函数y=![]() (x<0)的图象经过矩形OABC的对角线AC的中点M,分别与AB,BC交于点D、E,若BD=3,OA=4,则k的值为_____.
(x<0)的图象经过矩形OABC的对角线AC的中点M,分别与AB,BC交于点D、E,若BD=3,OA=4,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )
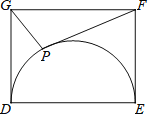
A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).



图① 图② 图③
查看答案和解析>>
科目:初中数学 来源: 题型:
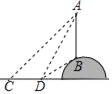
【题目】如图,为了测量小山顶的铁塔AB高度,王华和杨丽在平地上的C点处测得A点的仰角为45°,向前走了18m后到达D点,测得A点的仰角为60°,B点的仰角为30°
(1)求证:AB=BD;
(2)求证铁塔AB的高度.(结果精确到0.1米,其中![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,BO、CO是角平分线.
(1)∠ABC=50°,∠ACB=60°,求∠BOC的度数,并说明理由.
(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC的度数.
(3)若∠A=n°,求∠BOC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com