
【题目】问题提出
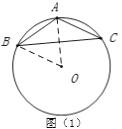
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
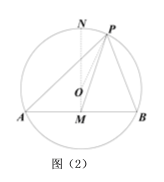
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
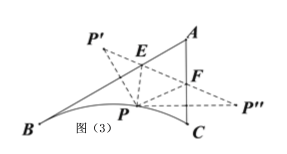
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).



图① 图② 图③
【答案】(1)5;(2)18;(3)(3![]() -9)km.
-9)km.
【解析】(1)如图(1),设外接圆的圆心为O,连接OA, OB,根据已知条件可得△AOB是等边三角形,由此即可得半径;
(2)如图(2)所示,连接MO并延长交⊙O于N,连接OP,显然,MN即为MP的最大值,根据垂径定理求得OM的长即可求得MN的最大值;
(3) 如图(3)所示,假设P点即为所求点,分别作出点P关于AB、AC的对称点P、P"连接PP、PE,PE,P"F,PF,PP",则PP"即为最短距离,其长度取决于PA的长度, 根据题意正确画出图形,得到点P的位置,根据等边三角形、勾股定理等进行求解即可得PE+EF+FP的最小值.
(1)如图(1),设外接圆的圆心为O,连接OA, OB,
∵O是等腰三角形ABC的外心,AB=AC,
∴∠BAO=∠OAC=![]() ∠BAC=
∠BAC=![]() =60°,
=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴OB=AB=5,
故答案为:5;
(2)如图(2)所示,连接MO并延长交⊙O于N,连接OP,
显然,MP≤OM+OP=OM+ON=MN,ON=13,OM=![]() =5,MN=18,
=5,MN=18,
∴PM的最大值为18;
(3) 如图(3)所示,假设P点即为所求点,分别作出点P关于AB、AC的对称点P、P"连接PP、PE,PE,P"F,PF,PP"
由对称性可知PE+EF+FP=PE+EF+FP"=PP",且P、E、F、P"在一条直线上,所以PP"即为最短距离,其长度取决于PA的长度,
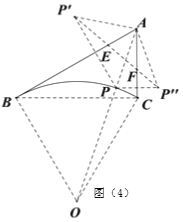
如图(4),作出弧BC的圆心O,连接AO,与弧BC交于P,P点即为使得PA最短的点,∵AB=6km,AC=3km,∠BAC=60°,
∴ABC是直角三角形,∠ABC=30°,BC=3![]() ,
,
BC所对的圆心角为60°,∴OBC是等边三角形,∠CBO=60°,BO=BC=3![]() ,
,
∴∠ABO=90°,AO=3![]() ,PA=3
,PA=3![]() -3
-3![]() ,
,
∠PAE=∠EAP,∠PAF=∠FAP",
∴∠PAP"=2∠ABC=120°,PA=AP",
∴∠APE=∠AP"F=30°,
∵PP"=2PAcos∠APE=![]() PA=3
PA=3![]() -9,
-9,
所以PE+EF+FP的最小值为3![]() -9km.
-9km.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了推动我县“三进校园”活动的广泛开展,引导学生走向操场,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)本次调查获取的样本数据的众数为 ,中位数为 ;
(3)根据样本数据,若学校计划购买![]() 双运动鞋,建议购买
双运动鞋,建议购买![]() 号运动鞋 双.
号运动鞋 双.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=13,BC=14,AC=15,点D在AC上(可与点A,C重合),分别过点A、C作直线BD的垂线,垂足为E,F,则AE+CF的最大值为_____,最小值为_____.
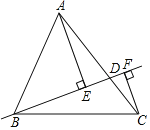
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人去年水果批发市场采购苹果,他看中了![]() 、
、![]() 两家苹果.这两家苹果品质一样,零售价都为6元/千克,批发价各不相同.
两家苹果.这两家苹果品质一样,零售价都为6元/千克,批发价各不相同.
(1)![]() 家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量超过1000千克且不超过2000千克,所有苹果按零售价的90%优惠;超过2000千克,所有苹果按零售价的88%优惠.
家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量超过1000千克且不超过2000千克,所有苹果按零售价的90%优惠;超过2000千克,所有苹果按零售价的88%优惠.
![]() 家的规定如下表:
家的规定如下表:
数量范围(千克) | 0—500 | 500以上—1500 | 1500以上—2500 | 2500以上 |
价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
表格说明:批发价格分段计算,如某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100-1500).
(1)如果他批发600千克苹果,那么他在![]() 、
、![]() 两家批发分别需要多少元?
两家批发分别需要多少元?
(2)如果他批发![]() 千克苹果(1500<
千克苹果(1500<![]() <2000),请你分别用含
<2000),请你分别用含![]() 的代数式表示在
的代数式表示在![]() 、
、![]() 两家批发所需的费用.
两家批发所需的费用.
(3)现在他要批发1800千克苹果,选择在哪家批发更优惠呢?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边三角形ABC的顶点B、C的坐标分别为(0,0)和(0,4).
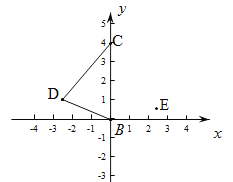
(1)求顶点A的坐标.
(2)D为第二象限内一点,作出点P,使得P到DB和DC的距离相等,且到点E的距离等于DB(不写作法,保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.
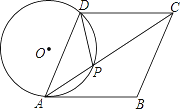
(1)求证:AB是⊙O的切线;
(2)若AC=8,tan∠BAC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,随着新能源汽车推广力度加大,产业快速发展,越来越多的消费者开始接受并购买新能源汽车,我国新能源汽车的生产量和销售量都大幅增长,下图是2014-2017年新能源汽车生产和销售的情况:根据统计图中提供的信息,预估全国2018年新能源汽车销售量约为__________万量,你的预估理由是____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com