
【题目】如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.
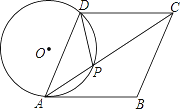
(1)求证:AB是⊙O的切线;
(2)若AC=8,tan∠BAC=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)见解析;(2)![]() .
.
【解析】(1)连结OP、OA,OP交AD于E,由PA=PD得弧AP=弧DP,根据垂径定理的推理得OP⊥AD,AE=DE,则∠1+∠OPA=90°,而∠OAP=∠OPA,所以∠1+∠OAP=90°,再根据菱形的性质得∠1=∠2,所以∠2+∠OAP=90°,然后根据切线的判定定理得到直线AB与⊙O相切;
(2)连结BD,交AC于点F,根据菱形的性质得DB与AC互相垂直平分,则AF=4,tan∠DAC=![]() ,得到DF=2
,得到DF=2![]() ,根据勾股定理得到AD=
,根据勾股定理得到AD=![]() =2
=2![]() ,求得AE=
,求得AE=![]() ,设⊙O的半径为R,则OE=R﹣
,设⊙O的半径为R,则OE=R﹣![]() ,OA=R,根据勾股定理列方程即可得到结论.
,OA=R,根据勾股定理列方程即可得到结论.
(1)连结OP、OA,OP交AD于E,如图,
∵PA=PD,∴弧AP=弧DP,∴OP⊥AD,AE=DE,∴∠1+∠OPA=90°.
∵OP=OA,∴∠OAP=∠OPA,∴∠1+∠OAP=90°.
∵四边形ABCD为菱形,∴∠1=∠2,∴∠2+∠OAP=90°,∴OA⊥AB,
∴直线AB与⊙O相切;
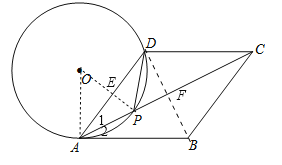
(2)连结BD,交AC于点F,如图,
∵四边形ABCD为菱形,∴DB与AC互相垂直平分.
∵AC=8,tan∠BAC=![]() ,∴AF=4,tan∠DAC=
,∴AF=4,tan∠DAC=![]() =
=![]() ,
,
∴DF=2![]() ,∴AD=
,∴AD=![]() =2
=2![]() ,∴AE=
,∴AE=![]() .
.
在Rt△PAE中,tan∠1=![]() =
=![]() ,∴PE=
,∴PE=![]() .
.
设⊙O的半径为R,则OE=R﹣![]() ,OA=R.
,OA=R.
在Rt△OAE中,∵OA2=OE2+AE2,∴R2=(R﹣![]() )2+(
)2+(![]() )2,
)2,
∴R=![]() ,即⊙O的半径为
,即⊙O的半径为![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
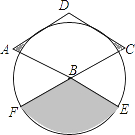
【题目】如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E,F,则图中阴影部分的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校园的学子餐厅把![]() 密码做成了数学题,小亮在餐厅就餐时,思索了一会,输入密码,顺利地连接到了学子餐厅的网络.
密码做成了数学题,小亮在餐厅就餐时,思索了一会,输入密码,顺利地连接到了学子餐厅的网络.
(1)如果![]() 是2,那么他输入的密码是___________.
是2,那么他输入的密码是___________.
(2)若他输入的密码是4235![]() ,最后两位被隐藏了,那么被隐藏的两位数是_____.
,最后两位被隐藏了,那么被隐藏的两位数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).



图① 图② 图③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
商店经营有A、B两种品牌的笔,A种笔的单价比B种笔的单价贵2元,若花140买A种笔,120元买B种笔,则A种笔反而比B种笔少一支.
(1)求A、B两种品牌的笔每支各多少元.
(2)某单位准备一次性购买两种笔共200支,预计费用不超过1800元.并且规定,A种笔的数量不能少于B种笔的![]() .问如何购买,单位花钱最少?最少花多少钱?
.问如何购买,单位花钱最少?最少花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当涂大青山有较为丰富的毛竹资源,某企业已收购毛竹110吨,根据市场信息,将毛竹直接销售,每吨可获利100元;如果对毛竹进行粗加工,每天可加工8吨,每吨可获利1000元;如果进行精加工,每天可加工![]() 吨,每吨可获利5000元,由于受条件限制,在同一天中只能采用一种方式加工,并且必须在一个月(30天)内将这批毛竹全部销售、为此研究了两种方案:
吨,每吨可获利5000元,由于受条件限制,在同一天中只能采用一种方式加工,并且必须在一个月(30天)内将这批毛竹全部销售、为此研究了两种方案:
(1)方案一:将收购毛竹全部粗加工后销售,则可获利________元;
方案二:30天时间都进行精加工,未来得及加工的毛竹,在市场上直接销售,则可获利________元.
(2)是否存在第三种方案,将部分毛竹精加工,其余毛竹粗加工,并且恰好在30天内完成?若存在,求销售后所获利润;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某九年一贯制学校在六年级和九年级的男生中分别随机抽取40名学生测量他们的身高,将数据分组整理后,绘制的频数分布直方图如下:其中两条纵向虚线上端的数值分别是每个年级抽出的40名男生身高的平均数,根据统计图提供的信息,下列结论不合理的是( )

A. 六年级40名男生身高的中位数在第153~158cm组
B. 可以估计该校九年级男生的平均身高比六年级的平均身高高出18.6cm
C. 九年级40名男生身高的中位数在第168~173cm组
D. 可以估计该校九年级身高不低于158cm但低于163cm的男生所占的比例大约是5%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD.
(1)求证:DB=DE;
(2)过点D作DF垂直BE,垂足为F,若CF=3,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
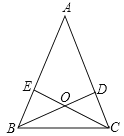
【题目】如图,锐角△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点O,且OB=OC
(1)求证:△ABC是等腰三角形;
(2)判定点O是否在∠BAC的角平分线上,说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com