
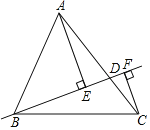
【题目】如图,在△ABC中,AB=13,BC=14,AC=15,点D在AC上(可与点A,C重合),分别过点A、C作直线BD的垂线,垂足为E,F,则AE+CF的最大值为_____,最小值为_____.
【答案】15 12
【解析】
设AE=m,CF=n,则m+n=y,用m、n及x表示出△ABD及△CBD的面积,根据S△ABC=S△ABD+S△CBD即可得到m+n关于x的反比例函数关系式.根据垂直线段最短的性质,当BD⊥AC时,x最小,由面积公式可求得;因为AB=13,BC=14,所以当BD=BC=14时,x最大.从而根据反比例函数的性质求出y的最大值和最小值.
设BD=x,AE+CF=y,AE=m,CF=n,则m+n=y,
∵由三角形面积公式,得![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
∵△ABC中AC边上的高为![]() ,
,
∴x的取值范围为![]() .
.
∵m+n随x的增大而减小,
∴当![]() 时,y的最大值为15,当x=14时,y的最小值为12.
时,y的最大值为15,当x=14时,y的最小值为12.
故答案为:15,12.


科目:初中数学 来源: 题型:
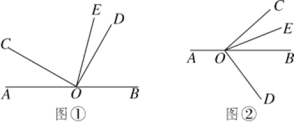
【题目】已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数.
(2)在图①中,若∠AOC=α,求∠DOE的度数(用含α的代数式表示).
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置,且保持射线OC在直线AB上方,在整个旋转过程中,当∠AOC的度数是多少时,∠COE=2∠DOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
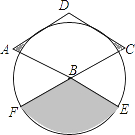
【题目】如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E,F,则图中阴影部分的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 相交于点
相交于点![]() ,
,![]() 分别为
分别为![]() 上的两点,
上的两点,![]() ,
,![]() ,分别交
,分别交![]() 于
于![]() 两点,连
两点,连![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④ ![]() ,其中正确的是( )
,其中正确的是( )

A. ①②B. ①④C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-2(m-1)x-m(m+2)=0
(1) 求证:此方程总有两个不相等的实数根
(2) 若x=-2是此方程的一个根,求实数m的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与○O相交于点D,连接BD,则∠DBC的大小为

A. 15° B. 35° C. 25° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校园的学子餐厅把![]() 密码做成了数学题,小亮在餐厅就餐时,思索了一会,输入密码,顺利地连接到了学子餐厅的网络.
密码做成了数学题,小亮在餐厅就餐时,思索了一会,输入密码,顺利地连接到了学子餐厅的网络.
(1)如果![]() 是2,那么他输入的密码是___________.
是2,那么他输入的密码是___________.
(2)若他输入的密码是4235![]() ,最后两位被隐藏了,那么被隐藏的两位数是_____.
,最后两位被隐藏了,那么被隐藏的两位数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).



图① 图② 图③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD.
(1)求证:DB=DE;
(2)过点D作DF垂直BE,垂足为F,若CF=3,求△ABC的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com