
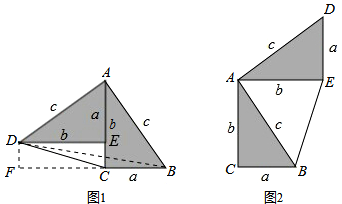
 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:分析 首先连结BD,过点B作DE边上的高BF,则BF=b-a,表示出S五边形ACBED,两者相等,整理即可得证.
解答 证明:连结BD,过点B作DE边上的高BF,则BF=b-a,
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab,
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),
∴$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),
∴a2+b2=c2.
故答案为:BD,点B作DE边上的高BF,BF=b-a,S△ACB+S△ABE+S△ADE=$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab,S△ACB+S△ABD+S△BDE=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),a2+b2=c2.
点评 此题考查了勾股定理的证明,用两种方法表示出五边形ACBED的面积是解本题的关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:选择题
| A. | (2$\sqrt{2}$)2=4 | B. | $\sqrt{\frac{5}{2}}$=$\frac{\sqrt{5}}{2}$ | C. | $\sqrt{{x}^{2}}$=x | D. | $\sqrt{-{x}^{3}}$=-x$\sqrt{-x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
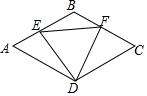 如图,在菱形ABCD中,E、F分别是AB、BC上一点,∠A=∠EDF=60°,有下列结论:①AE=BF,②△DEF 是等边三角形,③△BEF是等腰三角形,④∠ADE=∠BEF,其中正确的是( )
如图,在菱形ABCD中,E、F分别是AB、BC上一点,∠A=∠EDF=60°,有下列结论:①AE=BF,②△DEF 是等边三角形,③△BEF是等腰三角形,④∠ADE=∠BEF,其中正确的是( )| A. | ①② | B. | ②③④ | C. | ①②③④ | D. | ①②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com