
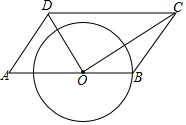
 如图,平行四边形ABCD中,O为AB上的一点,连接OD、OC,以O为圆心,OB为半径画圆,分别交OD,OC于点P,Q,若OB=2,OD=3,∠ADO=∠A,$\widehat{PQ}$=π,判断直线DC与⊙O的位置关系,并说明理由.
如图,平行四边形ABCD中,O为AB上的一点,连接OD、OC,以O为圆心,OB为半径画圆,分别交OD,OC于点P,Q,若OB=2,OD=3,∠ADO=∠A,$\widehat{PQ}$=π,判断直线DC与⊙O的位置关系,并说明理由. 分析 先判断直线DC与⊙O的位置的关系,然后根据题目中的数量关系可以求得点O到直线DC的距离,然后与圆的半径对比即可解答本题.
解答 解:直线DC与⊙O的位置关系是相离,
理由:∵OB=2,OD=3,∠ADO=∠A,
∴OA=OD=3,
∴AB=OA+OB=5,
∵四边形ABCD是平行四边形,
∴AB=DC=5,
∵$\widehat{PQ}$=π,
∴$π=\frac{nπ×2}{180}$,得n=90,
即∠DOC=90°,
∴OC=$\sqrt{D{C}^{2}-O{D}^{2}}=4$,
∴点O到DC的距离为:$\frac{3×4}{5}=2.4$,
∵2.4>2,
∴直线DC与⊙O的位置关系是相离.
点评 本题考查直线与圆的位置关系、平行四边形的性质,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:填空题
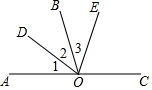 如图,O是直线AC上一点,OB,OD,OE为射线,OD平分∠AOB,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=65°,则∠1=15度.
如图,O是直线AC上一点,OB,OD,OE为射线,OD平分∠AOB,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=65°,则∠1=15度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
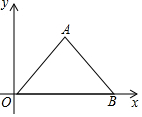 如图,在平面直角坐标系中,△AOB为等腰直角三角形A(4,4),点C从O出发,以2个单位/秒的速度沿x轴正方向运动.
如图,在平面直角坐标系中,△AOB为等腰直角三角形A(4,4),点C从O出发,以2个单位/秒的速度沿x轴正方向运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
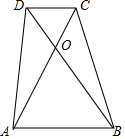 如图,在梯形ABCD中.DC∥AB.对角线AC,BD交于O点,设S△ODC=S1,S△AOB=S2,求证:S梯形ABCD=($\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$)2.
如图,在梯形ABCD中.DC∥AB.对角线AC,BD交于O点,设S△ODC=S1,S△AOB=S2,求证:S梯形ABCD=($\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$)2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com