练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在△ABC中，AB＝AC＝5，BC＝6，若点P在边AC上移动，则BP的最小值是（　　）

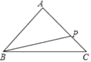
    A. 5 B. 6 C. 4 D. 4.8

    【答案】D

    【解析】

    根据点到直线的连线中，垂线段最短，得到当BP垂直于AC时，BP的长最小，过A作等腰三角形底边上的高AD，利用三线合一得到D为BC的中点，在直角三角形ADC中，利用勾股定理求出AD的长，进而利用面积法即可求出此时BP的长．

    根据垂线段最短，得到BP⊥AC时，BP最短，

    过A作AD⊥BC，交BC于点D，

    ∵AB＝AC，AD⊥BC，

    ∴D为BC的中点，又BC＝6，

    ∴BD＝CD＝3，

    在Rt△ADC中，AC＝5，CD＝3，

    根据勾股定理得：AD＝＝4，

    又∵S△ABC＝BCAD＝BPAC，

    ∴BP＝＝4.8．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在图1、图2的网格中，每个小四边形均为正方形，且边长是1．如果三角形的顶点均在网格交点处，我们称这样的三角形为格点三角形．下面的三角形均为格点三角形．

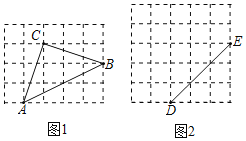
    （1）如图1，试判断△ABC的形状，并说明理由；

    （2）在图2的网格中，请你以DE为底边，画一个面积为7.5的等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】出租车司机王师傅某天早上营运时是在东西走向的大街上进行的，如果规定向东为正，向西为负，他这天早上所接六位乘客的行车里程()如下：

    2，+5，-4，+1，-6，-2

    (1)将最后一位乘客送到目的地时，王师傅在早上出发点的什么位置?

    (2)若汽车耗油量为，这天早上王师傅接送乘客，出租车共耗油多少升?

    (3)若出租车起步价为6元，起步里程为 (包括)，超过部分(不足按计算)每千米1．5元，王师傅这天早上共得车费多少元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】按图填空，并注明理由．

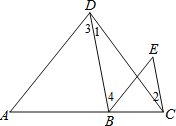
    已知：如图，∠1＝∠2，∠3＝∠E．

    求证：AD∥BE．

    证明：∵∠1＝∠2 （已知）

    ∴_____∥_____

    （________）

    ∴∠E＝∠_____

    （________）

    又∵∠E＝∠3 （ 已知 ）

    ∴∠3＝∠_____

    （________）

    ∴AD∥BE．

    （________）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

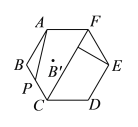
    【题目】如图所示，正六边形的边长为，点从点出发沿运动至点，点是点关于直线对称的点．

    （）点从点运动至过程中，下列说法正确的有__________．（填序号）

    ①当点运动到时，线段长为．

    ②点沿直线从运动到．

    ③点沿圆弧从运动到．

    （）点从点运动至的过程中，点到的距离的最小值是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

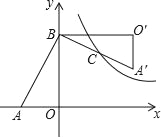
    【题目】如图，在Rt△AOB中，直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，将△AOB绕点B逆时针旋转90°后，得到△A′O′B，且反比例函数y=的图象恰好经过斜边A′B的中点C，若SABO=4，tan∠BAO=2，则k=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

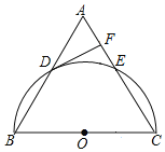
    【题目】如图，△ABC为等腰三角形，AC=BC，以边BC为直径的半圆与边AB，AC分别交于D，E两点，过点D作DF⊥AC，垂足为点F

    （1）判断DF与⊙O的位置关系，并证明你的结论；

    （2）若DF=3，EF=1，求弦EC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．求证：CE＝CF；

    （2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD．

    （3）运用（1）（2）解答中所积累的经验和知识，完成下题：

    如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE="10," 求直角梯形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，∠A＝∠C＝90°，BE平分∠ABC，DF平分∠CDA．

    (1)求证：BE∥DF；

    (2)若∠ABC＝56°，求∠ADF的大小．

    查看答案和解析>>

    同步练习册答案