
【题目】定义:长宽比为![]() :1(n为正整数)的矩形称为
:1(n为正整数)的矩形称为![]() 矩形.
矩形.
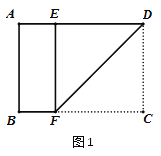
(1)如图1所示,将一张矩形纸片ABCD进行如下操作:将点C沿着过点D的直线折叠,使折叠后的点C落在边AD上的点E处,折痕为DF,通过测量发现DF=AD,则矩形ABCD是![]() 矩形吗?请说明理由.
矩形吗?请说明理由.
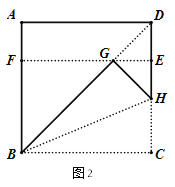
(2)我们可以通过折叠的方式折出一个![]() 矩形,如图2所示.操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.所得四边形BCEF为
矩形,如图2所示.操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.所得四边形BCEF为![]() 矩形,请说明理由.
矩形,请说明理由.
【答案】(1)矩形ABCD是![]() 矩形,理由见解析;
矩形,理由见解析;
(2)理由见解析.
【解析】试题分析:(1)根据四边形ABCD是![]() 矩形的定义,只要证明AD=
矩形的定义,只要证明AD=![]() CD即可.(2)设正方形ABCD的边长为1,求出BF的长即可解决问题.
CD即可.(2)设正方形ABCD的边长为1,求出BF的长即可解决问题.
试题解析:(1)四边形ABCD是![]() 矩形。
矩形。
理由:∵四边形ABCD是矩形,
∴∠EDC=∠DEF=∠C=90°,
∵DE=DC,
∴四边形CDEF是正方形。
∴DF=![]() DC,∵AD=DF
DC,∵AD=DF
∴AD=![]() DC,
DC,
∴矩形ABCD是2√矩形。
(2)设正方形ABCD的边长为1,则BD=![]() .
.
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形。
∴∠A=∠BFE,
∴EF∥AD,
∴BGBD=BFAB,即![]() =
=![]() ,
,
∴BF=![]() ,
,
∴BC:BF=1: ![]() =
=![]() :1,
:1,
∴四边形BCEF为![]() 矩形。
矩形。


科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=C,试猜想a,b,c之间的一种关系,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣2x2经过平移得到y=﹣2(x+1)2﹣3,平移方法是( )
A.向左平移1个单位,再向下平移3个单位B.向左平移1个单位,再向上平移3个单位
C.向右平移1个单位,再向下平移3个单位D.向右平移1个单位,再向上平移3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在矩形ABCD中,AD=60cm,CD=120cm,E、F为AB边的三等分点,以EF为边在矩形内作等边三角形MEF,N为AB边上一点,EN=10cm;
请在矩形内找一点P,使△PMN为等边三角形(画出图形,并直接写出△PMF的面积).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=BD;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1、a2、a3、a4、…满足下列条件:a1=﹣1,a2=﹣|a1+2|,a3=﹣|a2+3|,a4=﹣|a3+4|,…,an+1=﹣|an+n+1|(n为正整数)依此类推,则a2019的值为( )
A. ﹣1009B. ﹣1010C. ﹣2019D. ﹣2020
查看答案和解析>>
科目:初中数学 来源: 题型:
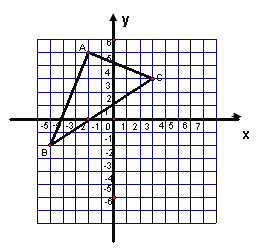
【题目】将△ABC向右平移4个单位长度,再向下平移5个单位长度,
(1)在图上画出对应的三角形A1B1C1;
(2)写出点A1、B1、C1的坐标.
(3)求出△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】环境空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为( )
A.2.5×10﹣5
B.2.5×105
C.2.5×10﹣6
D.2.5×106
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com