
����Ŀ����֪OΪֱ��MN��һ�㣬OP��MN���ڵ���Rt��ABO�У� ![]() ��AC��OP��OM��C��DΪOB���е㣬DE��DC��MN��E��
��AC��OP��OM��C��DΪOB���е㣬DE��DC��MN��E��
(1) ��ͼ1������B��OP�ϣ����AC OE(������������������������)�����߶�CA��CO��CD����ĵ�����ϵʽ�� ��
(2) ��ͼ1�еĵ���Rt��ABO��O��˳ʱ����ת(![]() )����ͼ2����ô(1)�еĽ��ۢ��Ƿ��������˵�����ɣ�
)����ͼ2����ô(1)�еĽ��ۢ��Ƿ��������˵�����ɣ�
(3) ��ͼ1�еĵ���Rt��ABO��O��˳ʱ����ת()��������ͼ3�л���ͼ�Σ���ֱ��д���߶�CA��CO��CD����ĵ�����ϵʽ ��

���𰸡���1����=����AC2+CO2=CD2����2����1���еĽ��ۢڲ����������ɼ���������3����ͼ��������OC-CA=![]() CD.
CD.
�������������������1������ͼ1��֤��AC=OC��OC=OE�ɵý��ۣ������ݹ��ɶ����ɵã�AC2+CO2=CD2����2����ͼ2����1���еĽ��������������������ߣ�����ȫ�������Σ�֤��A��D��O��C�ĵ㹲Բ������ACD=��AOB��ͬ���ã���EFO=��EDO����֤����ACO�ա�EOF����OE=AC��AO=EF�����ݹ��ɶ����ã�AC2+OC2=FO2+OE2=EF2����ֱ�������������Ϊб�߿ɵý��ۣ���3����ͼ3������AD����AD=OD֤����ACD�ա�OED��������CDE�ǵ���ֱ�������Σ���CE2=2CD2�����������ɵý��ۣ�OC��OE��2=��OC��AC��2=2CD2���������ǣ�OC��AC=![]() CD��
CD��
�����������1����AC=OE��
���ɣ���ͼ1�����ڵ���Rt��ABO�У���BAO=90�������ABO=��AOB=45����
��OP��MN�����COP=90�������AOC=45����
��AC��OP�����CAO=��AOB=45������ACO=��POE=90������AC=OC��
����AD��
��BD=OD����AD=OD��AD��OB����AD��OC�����ı���ADOC�������Σ����DCO=45����
��AC=OD�����DEO=45������CD=DE����OC=OE��
��AC=OE��
����Rt��CDO��
��CD2=OC2+OD2����CD2=AC2+OC2��
�ʴ�Ϊ��AC2+CO2=CD2��
��2����ͼ2����1���еĽ�������������
�����ǣ�
����AD���ӳ�CD��OP��F������EF��
��AB=AO��DΪOB���е㣬��AD��OB�����ADO=90����
�ߡ�CDE=90�������ADO=��CDE�����ADO����CDO=��CDE����CDO������ADC=��EDO��
�ߡ�ADO=��ACO=90�������ADO+��ACO=180������A��D��O��C�ĵ㹲Բ�����ACD=��AOB��
ͬ���ã���EFO=��EDO�����EFO=��AOC��
�ߡ�ABO�ǵ���ֱ�������Σ����AOB=45�������DCO=45�������COF����CDE�ǵ���ֱ�������Σ�
��OC=OF���ߡ�ACO=��EOF=90�������ACO�ա�EOF����OE=AC��AO=EF����AC2+OC2=FO2+OE2=EF2��
Rt��DEF��EF��DE=DC����AC2+OC2��DC2��
���ԣ�1���еĽ�������������
��3����ͼ3�����ۣ�OC��CA=![]() CD��
CD��
�����ǣ�����AD����AD=OD��
ͬ������ADC=��EDO��
�ߡ�CAB+��CAO=��CAO+��AOC=90�������CAB=��AOC��
�ߡ�DAB=��AOD=45�������DAB����CAB=��AOD����AOC��
����DAC=��DOE�����ACD�ա�OED����AC=OE��CD=DE�����CDE�ǵ���ֱ�������Σ�
��CE2=2CD2������OC��OE��2=��OC��AC��2=2CD2����OC��AC=![]() CD��
CD��
�ʴ�Ϊ��OC��AC=![]() CD��
CD��





 һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016���ҹ��ԡ�һ��һ·�����߹���ֱ��Ͷ��145����Ԫ����145���ÿ�ѧ��������ʾΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1������2.5����0.37��1.25������4��������8��
��2��2��7x2��8x+11������6x2��13x+12��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ABC=90�㣬
��1��������BCA��ƽ���ߣ���AB�ڵ�O���ó߹���ͼ����������ͼ�ۼ�����Ҫ��д��������
����OΪԲ�ģ�OBΪ�뾶��Բ��
��2������������ͼ�У�AC���O��λ�ù�ϵ���� ��
��3���ڣ�1���������£���BC=6��AB=8�����O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬѧ�μӡ���ʫ�ʴ����������α����ɼ���ƽ���ֶ���85�֣�����ױ����ɼ��ķ���ΪS��2=16.7���ұ����ɼ��ķ���ΪS��2=28.3����ô�ɼ��Ƚ��ȶ���������ס����ҡ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB����O��ֱ������E����O�ϣ�����E��ֱ��EF��AB���ӳ��߽����F��AC��EF������ΪC��AEƽ����FAC��
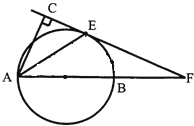
��1����֤��CF����O�����ߣ�
��2����F=30��ʱ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������꣬�й������ġ�һ��һ·��Ϊ���߹��Ҵ�����Լ180000����ҵ��λ����180000�ÿ�ѧ��������ʾΪ�� ��
A.1.8��105
B.1.8��104
C.0.18��106
D.18��104
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com